重力結合能是將鬆散物質通過引力作用相互聚攏的能量，其在量上等於將物體移動至無限遠處所需的能量，或者物體從無限遠處開始加速的過程中所釋放的能量（通常以熱能的形式）。

一個系統的重力結合能等於這個系統的重力勢能的相反數。在一個天體和一顆衛星的系統中，重力結合能較衛星與天體之間的重力勢能，其絕對值大得多。這是因為，後者僅將兩部分分離的能量計算在內，而不計算各部分本身的能量。

對於一個均質球體，重力結合能U的定義為：

U = \frac{(3/5)GM^2}{r}

其中，G代表重力常數，M是這個球體的質量，r是球體半徑。與將兩個相互接觸的相同球體分離至無限遠所需的能量相比，這一能量還要大20%。

假設，地球是一個均質球體，質量M=5.97×10²⁴kg，半徑r=6.37×10⁶m，那麼U就是2.24×10³²J。這大致上等於太陽一周所釋放的能量。它是37.5 MJ/kg，是表面上的勢能的60%。

根據緯里理論，一顆恆星的重力結合能大約是內部熱能的兩倍。

雖然萬有引力本身相對質量非常小，但是當總體質量很大時，比如地球，其因重力產生的能量就會變得不容忽視，現代科學家相信，地核的高溫，就與重力結合能有關

2 個分類：

萬有引力

能量

維基台北寫作聚於每月第二個禮拜六舉行，歡迎報名參與

[關閉]

宇宙速度

維基百科，自由的百科全書

A: 跌落地球
B: 跌落地球
C: 圓周運動 = 7.9km/s
D: 橢圓軌道
E: 逃逸 > 11.2km/s

宇宙速度（英語：cosmic velocity），是指物體從地球出發，要脫離天體重力場的四個較有代表性的初始速度的統稱。計算宇宙速度的基本公式如下：^[1]

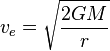
v_e = \sqrt{\frac{2GM}{r}}

太空飛行器按其任務的不同，需要達到這四個宇宙速度的其中一個。例如人類第一個發射成功的星際探測器月球1號就需要達到第二宇宙速度，才能擺脫地球重力。^[2]而旅行者2號則需要達到第三宇宙速度，才能離開太陽系。^[3]

逃逸速度

逃逸速度是指一物體的動能等於該物體的重力勢能的大小時的該物體的速率。逃逸速度一般描述為擺脫一重力場的引力束縛飛離那重力場所需的最低速率。對於「第一宇宙速度」和「第二宇宙速度」來說，「逃逸速度」這一用語可以認為是用詞不當，因為它實際上是速率，而不是速度，亦即是說，它表示該物體必須運動得多快，卻與運動方向無關，除了不是移向那重力場。更術語地說，逃逸速度是純量，而非向量。

逃逸速度的公式如下：^[1]

v_e = \sqrt{\frac{2GM}{r}} = \sqrt{\frac{2\mu}{r}} = \sqrt{2gr\,}

其中的 $v_e$ 是重心逃逸速度、 $G$ 是萬有引力常數， $M$ 是擺脫對象的質量， $r$ 是擺脫對象質心與逃逸物位置的距離， $g$ 是在該位置的重力加速度，而 ${\mu}$ 則是標準重力參數。^[4]

在某一特定高度上的逃逸速度是同一高度上公轉速度的 $\sqrt 2$ 倍。這對應著一個事實，即物體的勢能是其動能的負2倍，例如在太陽上的勢能和動能總和必須至少是零，才能達到逃逸速度。物體要達到繞地球飛行作圓周運動的速度被稱為第一宇宙速度，而地球的逃逸速度則被稱為第二宇宙速度。^[5]

逃逸速度的公式在加入常數後，會變成下列公式：

v_e \approx 2.364 \times 10^{-5} r \sqrt \rho.\,

第一宇宙速度

第一宇宙速度（first cosmic velocity），又稱為環繞速度，是指在地球上發射的物體繞地球飛行作圓周運動所需的最小初始速度。要作圓周運動，必須始終有一個力作用在太空飛行器上。其大小等於該太空飛行器運行線速度的平方乘以其質量再除以公轉半徑，即 $F=\frac{mv^2}{R}$ ，其中 $\frac{v^2}{R}$ 是物體作圓周運動的向心加速度。在這裡，正好可以利用地球的引力，在合適的軌道半徑和速度下，地球對物體的引力，正好等於物體作圓周運動的向心力。^[6]第一宇宙速度的計算公式是：

G\frac{Mm}{R^2} = m\frac{v_1^2}{R}

v_1 = \sqrt{\frac{GM}{R}} = 7.9 km/s

或者：

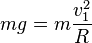
mg = m\frac{v_1^2}{R}

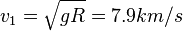
v_1 = \sqrt{gR} = 7.9 km/s

實際上，地球表面存在稠密的大氣層，太空飛行器不可能貼近地球表面作圓周運動，必需在150千米的飛行高度上，才能繞地球作圓周運動。在此高度下的環繞速度為7.8千米/秒。^[7]

第二宇宙速度

月球1號是首個達到第二宇宙速度的太空探測器^[8]

第二宇宙速度（second cosmic velocity），亦即地球的脫離速度，是指在地球上發射的物體擺脫地球引力束縛，飛離地球所需的最小初始速度。將無窮遠處的物體的勢能記為0，則距離地心為r的地方，勢能為 -GMm/r,那麼在地表的待發射的物體勢能為 -GMm/R。^[9]若要脫離地球的引力圈（即逃離地球），相當於要給該物體一定的動能來抵消它在地球表面的重力勢能 -GMm/R，恰好完全抵消時，即是逃離地球所需最小的速度（如下式）。

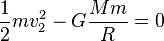
\frac12mv_2^2 - G\frac{Mm}{R} = 0

v_2 = \sqrt{\frac{2GM}{R}} = \sqrt{2gR} = 11.2 km/s

此外，也可以從能量守恆的角度來解釋上式：物體恰好逃離地球時速度為0，逃離地球後最終它會到達離地球無限遠處，因此有上式的動能和勢能之和為0。換句話說，假設太空船的飛行沒有阻力，那麼只要它在初始時刻達到第二宇宙速度，那麼就能保證它能夠逃離地球並最終到達離地球無限遠處，在初始時刻之後並不需要繼續提供能量。

然而，地球表面有稠密的大氣層，太空船飛行有阻力，並且難以達到這樣高的初始速度起飛。實際上，太空船是先離開大氣層，再加速完成脫離的（例如先抵達近地軌道，再在該軌道加速）。在這高度下，太空船的脫離速度較小，約為10.9公里/秒。^[10]實際上太空船的飛行速度遠比計算值要低得多，太空船尾部的噴射器持續地給予向上的推力分力，而這個力只要大於地球對太空船所施加的吸引力，即Δ >0,太空船就能脫離（或者說遠離）地球的引力場。因此亦有人認為，只要向上分力持續大於太空船重量，便可以相較微小許多的初速脫離地球的引力場，然而所花時間的加長，使得這在實際情形中並不佔優勢。^[11]

第三宇宙速度

第三宇宙速度（third cosmic velocity)，是指在地球上發射的物體擺脫太陽引力束縛，飛出太陽系所需的最小初始速度。本來，在地球軌道上，要脫離太陽引力所需的初始速度為42.1千米/秒，但地球繞太陽公轉時令地面所有物體已具有29.8千米/秒的初始速度，故此若沿地球公轉方向發射，只需在脫離地球引力以外額外再加上12.3千米/秒的速度。^[12]即物體所需的總動能為：

\frac12mv_3^2=\frac12mv_2^2+\frac12m \Delta v^2

由此得知所需速度為

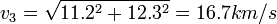
v_3=\sqrt{11.2^2+12.3^2}=16.7 km/s

第四宇宙速度

第四宇宙速度（fourth cosmic velocity），是指在地球上發射的物體擺脫銀河系引力束縛，飛出銀河系所需的最小初始速度。但由於人們尚未知道銀河系的準確大小與質量，因此只能粗略估算，其數值在525千米/秒以上。而實際上，仍然沒有太空飛行器能夠達到這個速度。^[13]

宇宙速度的概念也可應用於在其他天體發射太空飛行器的情況。例如計算火星的環繞速度和逃逸速度，只需要把公式中的M,R,g換成火星的質量、半徑、表面重力加速度即可。^[14]

數據表

離開地球的最低速度為11.2 km/s（約為40,320 km/h或25,000 mph）。但是，在地球軌道上，離開太陽系的最低速度卻是42.1 km/s 。

位置	擺脫對象	V_e^[15]	位置	擺脫對象	V_e^[15]
太陽	太陽引力	617.5 km/s
水星	水星引力	4.3 km/s	水星	太陽引力	67.7 km/s
金星	金星引力	10.3 km/s	金星	太陽引力	49.5 km/s
地球	地球引力	11.2 km/s	地球/月球	太陽引力	42.1 km/s
月球	月球引力	2.4 km/s	月球	地球引力	1.4 km/s
火星	火星引力	5.0 km/s	火星	太陽引力	34.1 km/s
木星	木星引力	59.5 km/s	木星	太陽引力	18.5 km/s
土星	土星引力	35.6 km/s	土星	太陽引力	13.6 km/s
天王星	天王星引力	21.2 km/s	天王星	太陽引力	9.6 km/s
海王星	海王星引力	23.6 km/s	海王星	太陽引力	7.7 km/s
銀河系	銀河系引力	≥ 525 km/s ^[16]
事件視界	黑洞引力	>299,792 km/s

因為地球擁有大氣層，所以在地表上不能達到地球的逃逸速度，即11.2 km/s（40,320 km/h）。這是因為這個速度遠超過極音速，並因此會導致大部份物體因氣動加熱而燃燒殆盡或被大氣阻力撕裂。因此，太空船是以逃逸軌道的方式離開地球。它們會先到達近地軌道（160–2,000 km）^[17]^[18]，然後加速至接近地球的逃逸速度：約10.9 km/s。儘管這裡仍然有速度變化，但因為其本身的速度已達8 km/s（28,800 km/h），所以其速度變化已被大大地減低了。^[19]