薛丁格方程式(英語:Schrödinger equation)是由奧地利物理學家薛丁格在1926年提出的一個用於描述量子力學中波函數的運動方程式[1],被認為是量子力學的奠基理論之一。
薛丁格方程式主要分為含時薛丁格方程式與不含時薛丁格方程式。含時薛丁格方程式相依於時間,專門用來計算一個量子系統的波函數,怎樣隨著時間演變。不含時薛丁格方程式不相依於時間,可以計算一個定態量子系統,對應於某本徵能量的本徵波函數。波函數又可以用來計算,在量子系統裏,某個事件發生的機率幅。而機率幅的絕對值的平方,就是事件發生的機率密度。
薛丁格方程式的解答,清楚地描述量子系統裏,量子尺寸粒子的統計性量子行為。量子尺寸的粒子包括基本粒子,像電子、質子、正子、等等,與一組相同或不相同的粒子,像原子核。
薛丁格方程式可以轉換為海森堡的矩陣力學,或費曼的路徑積分表述 (path integral formulation) 。薛丁格方程式是個非相對論性的方程式,不能夠用於相對論性理論。海森堡表述比較沒有這麼嚴重的問題;而費曼的路徑積分表述則完全沒有這方面的問題。
[编辑] 含時薛丁格方程式
雖然,含時薛丁格方程式能夠啟發式地從幾個假設導引出來。理論上,我們可以直接地將這方程式當作一個基本假定。在一維空間裏,一個單獨粒子運動於位勢 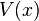 中的含時薛丁格方程式為
中的含時薛丁格方程式為
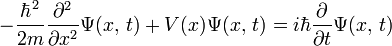 ;(1)
;(1)
其中,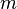 是質量,
是質量,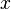 是位置,
是位置,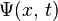 是相依於時間
是相依於時間  的波函數,
的波函數,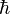 是約化普朗克常數,
是約化普朗克常數,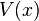 是位勢。
是位勢。
類似地,在三維空間裏,一個單獨粒子運動於位勢  中的含時薛丁格方程式為
中的含時薛丁格方程式為
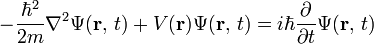 。(2)
。(2)
假若,系統內有  個粒子,則波函數是定義於
個粒子,則波函數是定義於  -位形空間,所有可能的粒子位置空間。用方程式表達,
-位形空間,所有可能的粒子位置空間。用方程式表達,
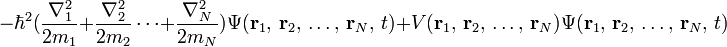
 。
。
其中,波函數  的第
的第 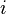 個參數是第
個參數是第 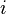 個粒子的位置。所以,第
個粒子的位置。所以,第 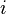 個粒子的位置是
個粒子的位置是  。
。
[编辑] 不含時薛丁格方程式
不含時薛丁格方程式不相依於時間,又稱為本徵能量薛丁格方程式,或定態薛丁格方程式。顧名思義,本徵能量薛丁格方程式,可以用來計算粒子的本徵能量與其它相關的量子性質。
應用分離變數法,猜想 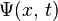 的函數形式為
的函數形式為
 ;
;
其中, 是分離常數,
是分離常數, 是對應於
是對應於  的函數.稍回兒,我們會察覺
的函數.稍回兒,我們會察覺  就是能量.
就是能量.
代入這猜想解,經過一番運算,含時薛丁格方程式 (1) 會變為不含時薛丁格方程式:
 。
。
類似地,方程式 (2) 變為
 。
。
[编辑] 歷史背景與發展
愛因斯坦詮釋普朗克的量子為光子,光波的粒子;也就是說,光波具有粒子的性質,一種很奇奧的波粒二象性。他建議光子的能量與頻率成正比。在相對論裏,能量與動量之間的關係跟頻率與波數之間的關係相同,所以,連帶地,光子的動量與波數成正比。
1924年,路易·德布羅意提出一個驚人的假設,每一種粒子都具有波粒二象性。電子也有這種性質。電子是一種波動,是電子波。電子的能量與動量決定了它的物質波的頻率與波數。1927年,柯林頓·戴維孫和雷斯特·革末將緩慢移動的電子射擊於鎳晶體標靶。然後,測量反射的強度,偵測結果與X射線根據布拉格定律 (Bragg's law) 計算的繞射圖案相同。戴維森-革末實驗徹底的證明了德布羅意假說。
薛丁格夜以繼日地思考這些先進理論,既然粒子具有波粒二象性,應該會有一個反應這特性的波動方程式,能夠正確地描述粒子的量子行為。於是,薛丁格試著尋找一個波動方程式。哈密頓先前的研究引導著薛丁格的思路,在牛頓力學與光學之間,有一種類比,隱蔽地暗藏於一個察覺裏。這察覺就是,在零波長極限,實際光學系統趨向幾何光學系統;也就是說,光射線的軌道會變成明確的路徑,遵守最小作用量原理。哈密頓相信,在零波長極限,波傳播會變為明確的運動。可是,他並沒有設計出一個方程式來描述這波行為。這也是薛丁格所成就的。他很清楚,經典力學的哈密頓原理,廣為學術界所知地,對應於光學的費馬原理。藉著哈密頓-亞可比方程式,他成功地創建了薛丁格方程式。薛丁格用自己設計的方程式來計算氫原子的譜線,得到了與用波耳模型計算出的能級相同的答案。
但是,薛丁格對這結果並不滿足,因為,索末菲似乎已經正確地計算出氫原子光譜線精細結構常數的相對論性的修正。薛丁格試著用相對論的能量動量關係式,來尋找一個相對論性方程式(現今稱為克萊因-戈登方程式),可以描述電子在庫侖位勢內的量子行為。薛丁格計算出這方程式的定態波函數。可是,相對論性的修正與索末菲的公式有分歧。雖然如此,他認為先前非相對論性的部分,仍舊含有足夠的新結果。因此,決定暫時不發表相對論性的修正,只把他的波動方程式與氫原子光譜分析結果,寫為一篇論文。1926年,正式發表於物理學界[2]。從此,給予了量子力學一個新的發展平台。
薛丁格方程式漂亮地解釋了 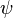 的行為,但並沒有解釋
的行為,但並沒有解釋 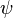 的意義。薛丁格曾嘗試解釋
的意義。薛丁格曾嘗試解釋 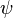 代表電荷的密度,但卻失敗了。1926年,就在薛丁格第四篇的論文發表之後幾天,馬克斯·玻恩提出機率幅的概念,成功地解釋了
代表電荷的密度,但卻失敗了。1926年,就在薛丁格第四篇的論文發表之後幾天,馬克斯·玻恩提出機率幅的概念,成功地解釋了 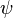 的物理意義[3]。可是,薛丁格本人一直不承認這種統計或機率的表示方法,和它所伴隨的非連續性波函數塌縮。就像愛因斯坦的認為量子力學是基本為確定性理論的統計近似,薛丁格永遠無法接受哥本哈根詮釋。在他有生最後一年,他寫給馬克斯·玻恩的一封信內,薛丁格清楚地表明了這看法。
的物理意義[3]。可是,薛丁格本人一直不承認這種統計或機率的表示方法,和它所伴隨的非連續性波函數塌縮。就像愛因斯坦的認為量子力學是基本為確定性理論的統計近似,薛丁格永遠無法接受哥本哈根詮釋。在他有生最後一年,他寫給馬克斯·玻恩的一封信內,薛丁格清楚地表明了這看法。