
A contour plot of the effective
potential of a two-body system due to gravity and inertia at one point in time.希爾球是分別環繞著這兩個大質量天體的圓型區域。
希爾球,粗略的說,是環繞在天體(像是行星)周圍的體積,那裡被它吸引的天體(像是衛星)受到它的控制,而不是被它繞行的較大天體(像是恆星)所控制。因此,行星能保留住衛星,而衛星的軌道必須在行星的希爾球內。同樣的,月球也會有它的希爾球,任何位於月球的希爾球內的天體將會成為月球的衛星,而不是地球的衛星。
更精確的說,希爾球接近於一個小天體在面對著一個大許多的天體的重力影響下,只會受到攝動影響的引力球範圍。這是美國天文學家喬治·威廉·希爾以法國天文學家愛德華·洛希的工作為基礎所定義的,由於這個緣故,它有時也被稱為洛希球。
為了說明,考慮木星環繞著太陽的具體事例,對太空中任何的點,可以計算下面三種力的總和:
- 來自太陽的引力,
- 來自木星的引力,
- 在有著與木星相同頻率的點上,繞著太陽運轉的微粒所受到的離心力。
木星的希爾球是以木星為中心,這三種力量的總和永遠都指向木星的最大的球。以一般的用語來說,它是圍繞在繞著主要天體的次要天體週圍的球形,在這個球形內的淨力是一個指向次要天體的向心力。因此,希爾球在我們的例子中是描述一顆小的天體,像是衛星或人造衛星可以在木星附近穩定的繞著木星運轉,而不會單純的進入橢圓軌道繞著太陽運轉的最大極限範圍。
在兩個天體的連線方向上,希爾球的邊界在拉格朗日點的L1和L2,這也是次要天體的影響力最短的方向,並且以此做為希爾球大小的限制因素。超越了這個距離,第三個天體環繞著次要天體(此處以木星為例)的軌道就至少會有一部分逸出了希爾球,並且將會受到主要天體(此例中為太陽)漸增的潮汐力攝動,最後終將繞著後者運轉。
雖然都是與洛希有關的術語,但洛希球絕不能和洛希極限或是洛希瓣混淆在一起。洛希極限是僅由重力維繫的物體受到潮汐力作用開始被破壞的距離;洛希瓣描述的是一個環繞在兩個天體周圍的軌道,會造成這兩個天體競逐捕獲這個天體的距離界限。
[编辑] 公式和例子
如果較小的天體(例如地球)質量是m,被它環繞的較重的天體(例如太陽)質量是M,軌道半長軸是a,離心率是e,則較小天體(例如地球)的希爾球半徑r的近似值為 [1]:
![r \approx a (1-e) \sqrt[3]{\frac{m}{3 M}}](http://upload.wikimedia.org/wikipedia/zh/math/5/0/f/50fc57604cad722d8fae9e49a0544d13.png)
當離心率可以忽略時(最有利於穩定軌道的論點),公式可以簡化為:
![r \approx a \sqrt[3]{\frac{m}{3M}}](http://upload.wikimedia.org/wikipedia/zh/math/5/c/f/5cf96e48a1d82de12814b75962e3156a.png)
在地球的例子中,地球質量為5.97×1024公斤,以1.496億公里的距離環繞著質量1.99×1030公斤的太陽,希爾球的半徑大約是150萬公里(0.01天文單位)。月球繞地球的軌道平均距離為38萬4,000公里,很安穩的在地球引力的勢力範圍內,沒有被扯入獨立繞行太陽軌道的危險或顧慮。根據軌道的周期:地球所有穩定的衛星,它的軌道週期必須短於7個月。
早先(省略調離心率)的公式可以再改以下面的形式呈現:

如此的表示法將希爾球的體積與次要天體環繞主要天體的軌道體積做了比較上的聯繫。具體的說,質量的比率是這兩個球體積比值的三倍。
快速的估計希爾球半徑的方法是將上述等式中的質量用密度來取代:
![\frac{r}{R_{secondary}} \approx \frac{a}{R_{primary}} \sqrt[3]{\frac{\rho_{secondary}}{3 \rho_{primary}}} \approx \frac{a}{R_{primary}}](http://upload.wikimedia.org/wikipedia/zh/math/1/d/7/1d7a399c8b32e279840a13630658b494.png)
此處ρsecond和ρprimary分別是主要天體和次要天體的密度,並且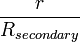 和
和 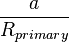 是它們的半徑。第二個公式在太陽系內大部分的事例中都與事實大略相符,
是它們的半徑。第二個公式在太陽系內大部分的事例中都與事實大略相符,![\sqrt[3]{\frac{\rho_{secondary}}{3 \rho_{primary}}}](http://upload.wikimedia.org/wikipedia/zh/math/b/d/4/bd4d6d2d6fa8bfe4407c2a13762205e6.png) 的值都接近1(地-月系統是最大的例外,並且大多數的土星衛星都在20%之內。) 這是很方便的型式,因此許多天文學家都記住行星的半徑,並以此為單位進行計算的工作。
的值都接近1(地-月系統是最大的例外,並且大多數的土星衛星都在20%之內。) 這是很方便的型式,因此許多天文學家都記住行星的半徑,並以此為單位進行計算的工作。
[编辑] 真實穩定的區域
希爾球只是估計的大小,因為還有其它的力(像是輻射壓和亞爾科夫斯基效應)也會造成攝動使它逸出到球外。第三個天體的質量也必須夠小,才不致於因為自身的引力影響而使情形變得複雜。詳細的數值計算顯示,軌道在或正好在希爾球內的天體,在長遠看來仍是不穩定的;看起來穩定的衛星軌道半徑只在希爾球半徑的1/2或1/3的範圍之內(逆行軌道似乎比順行軌道穩定)。
[编辑] 更多的例子
太空人不可能在地球上空300公里之處圍繞著太空梭(質量大約104公噸)運轉,因為希爾球的半徑只有120公分,遠比太空梭本身還要小。事實上,任何一顆低地球軌道衛星(高度 1,400公里),密度必須是鉛的800倍以上(9102.6 g/cm3),才可能擁有自己的希爾球,否則它將不足以勝任支持任何的軌道。(鉛的密度是11.34 g/cm3,地球質量為 5.9742×1024kg。一顆球形的同步衛星將需要鉛密度的5倍足以維繫自己的衛星,這樣的衛星密度是地球上自然產物中密度最高的元素銥的2.5倍(同步軌道的高度是35,786 公里,銥的密度是22.65 g/cm3)。只有在兩倍於同步軌道的高度上,一顆鉛球可以維繫自身的衛星軌道;由於月球的軌道遠大於同步軌道距離的2倍以上,因此環繞月球的軌道是存在的。
在太陽系,海王星有著最大的希爾球,半徑是1億1,600萬公里,或是0.775天文單位;因為他與太陽距離的遙遠,充分的補償了它的質量低於木星的不足,木星的希爾球半徑只有5,300萬公里。 主帶小行星中的榖神星,希爾球的半徑只有22萬公里。因為質量的迅速減少,有一顆衛星的1994 KW4,是接近水星的小行星,希爾球的半徑為22公里。
[编辑] 推導
一個不很嚴謹,但概念上是正確的可以推導出希爾球半徑,就是可以利用人造衛星環繞一個天體(例如行星)的軌道角速度和這個天體本身環繞母天體的軌道角速度相等,這粗略的是恆星重力影響與行星相等的半徑。這在數量級上的數值精確度上是正確的。
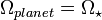
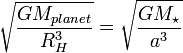
此處RH 是希爾球半徑,a是行星環繞恆星的半長軸。以一些基本的符號:
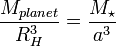
得到的希爾球半徑為:
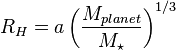
[编辑] 相關條目
洛希瓣
维基百科,自由的百科全书
洛希瓣是包圍在恆星周圍的空間,在這個範圍內的物質會受到該天體的引力約束而在軌道上環繞著。如果恆星膨脹至洛希瓣的範圍之外,這些物質將會擺脫掉恆星引力的束縛。如果這顆恆星是聯星系統,則這些物質會經由內拉格朗日點落入伴星的範圍內。等位面的臨界引力邊界形狀類似淚滴形,淚滴形的尖端指向另一顆伴星 (尖端位於系統的L1拉格朗日點)。它不同於洛希極限,後者是僅由引力維繫在一起的物質受到潮汐力作用開始崩解的距離;它也與洛希球不同,那是在一個天體周圍的空間,在受到另一個它所環繞的更巨大天體的攝動時,仍能維持小天體的軌道穩定,接近球形的引力球。洛希瓣、洛希極限和洛希球都是以法國天文學家愛德華·洛希的名字命名的。
[编辑] 洛希瓣的定義
在有著圓軌道的聯星系統中,它通常能在隨著天體一起轉動的座標系統中很有效的描述。在這些非慣性系統,除了重力之外還必須考慮離心力。可以用位能已起描述這兩種力,因此,例如,恆星的表面可以沿著等位面表面伸展。
在靠近個別的恆星時,相同的重力等位面形狀是接近球形的,並且與考進的恆星是同心球。在離恆星系統較遠處,等位面的形狀接近橢球體,並且延伸的方向平行於兩顆恆星的聯心軸線的方向。臨界的等位面和系統本身的L1拉格朗日點相交會,在各自瓣圖中形成在兩顆恆星之間的8字形瓣圖。這個臨界的等位面定義出洛希瓣[1]。
當相對於共同轉動系統中的物質流動時,似乎會採取像科氏力的行為。這不是從洛希瓣的模型推導倒出來的,科氏力是不守恆力 (也就是說,不能以純量來處理)。
[编辑] 質量轉移
當一顆恆星"超越了洛希瓣",它的表面擴展至洛希瓣之外,同時超越過洛希瓣的物質會經由L1拉格朗日點掉落至伴星的落希瓣之內。在聯星演化的過程中,這種質量傳輸被稱為洛希瓣溢流 (洛希瓣超流)。
原則上,質量傳輸可能導致天體完全的解體,因為質量的減少會導致落希瓣的萎縮。但是,有幾個原因使這種情況通常不至於發生。首先,捐助恆星的質量減縮會導致捐助者的縮小,這可能會阻礙後續的捐助。其次,在聯星的兩顆恆星之間的質量傳輸還包括了角動量的傳輸。當物質從質量較大的恆星捐助給原本質量較小的恆星增生時,通常會導致軌道的收縮,反過來造成聯星軌道的膨脹 (根據質量守恆和角動量守恆的設想)。聯星軌道的擴大將導致較少的戲劇性收縮,或甚至會擴大捐助者的洛希瓣,而這通常會阻止捐助者受到破壞。
要測量質量傳輸的穩定性和捐助者確實的萎縮,需要實際計算捐助恆星的半徑和之後的洛希瓣質量傳輸;如果恆星擴張的比洛希瓣的縮小還快,或是縮小的比 洛希瓣拖拉的時間還慢,質量的傳輸會變得不穩定而導致捐助恆星可能的瓦解。如果捐助恆星擴張的較慢,或是收縮得比洛希瓣快,質量的傳輸通常會保持穩定並且 可以持續很長的時間。
由於洛希瓣溢流的質量傳輸幾種易懂的天文現象之一,包括大陵五系統,再發新星 (包含一顆紅巨星和一顆白矮星的聯星,並且相距的距離組以使紅巨星的物質逐漸流動至白矮星)、X射線聯星和毫秒脈衝星。
[编辑] 洛希瓣的幾何
洛希瓣的精確形狀取決於質量比,並且必須經過數值的計算。但是,在多數的用途中,都使用形狀近似和有著相同體積的洛希瓣。一個有著球形和半徑的近似計算公式如下:
 for
for 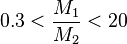
並且
 對於
對於 
此處,A是系統的半長軸,r1是環繞著質量為M1的洛希瓣的半徑。這些公式大約可以精確到2%以內[1]。
[编辑] 相關條目
波粒二象性
维基百科,自由的百科全书
波粒二象性(英語:Wave-particle duality)是微觀粒子的基本屬性之一。指微觀粒子有時顯示出波動性(這時粒子性不顯著),有時又顯示出粒子性(這時波動性不顯著),在不同條件下分別表現為波動和粒子的性質。一切微觀粒子都具有波粒二象性。
在古典力學中,研究對象總是被明確區分為「純」波動和「純」粒子。前者的典型例子是光,後者則組成了我們常說的「物質」。公元1905年,愛因斯坦提出了光電效應的光量子解釋,人們開始意識到光波同時具有波和粒子的雙重性質。公元1924年,德布羅意提出「物質波」假說,認為「一切物質」和光一樣都具有波粒二象性。根據這一假說,在「一切物質」的範圍之內的電子也會具有干涉和繞射(繞射)等波動現象,這被後來的戴維森-革末實驗所證實。
[编辑] 「波」和「粒子」的數學關係
物質的粒子性由能量 E 和動量 p 刻畫,波的特徵則由頻率 ν 和波長 λ 表達,這兩組物理量由普朗克常數 h 所聯繫。
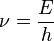

[编辑] 歷史
在十九世紀末,日臻成熟的原子論逐漸盛行,根據原子理論的看法,物質都是由微小的粒子——原子構成。比如原本被認為是一種流體的電,由約瑟夫·湯姆森的陰極射線實驗證明是由被稱為電子的粒子所組成。因此,人們認為大多數的物質是由粒子所組成。而與此同時,波被認為是物質的另一種存在方式。波動論已經被相當深入地研究,包括干涉和繞射等現象。由於光在托馬斯·楊的雙狹縫實驗中,以及夫琅禾費繞射中所展現的特性,明顯地說明它是一種波動。
不過在二十世紀來臨之時,這個觀點面臨了一些挑戰。1905年,由阿爾伯特·愛因斯坦研究的光電效應展示了光粒子性的一面。隨後,電子繞射被預言和證實了。這又展現了原來被認為是粒子的電子波動性的一面。
這個波與粒子的困擾終於在二十世紀初由量子力學的建立所解決,即所謂波粒二象性。他提供了一個理論框架,使得任何物質在一定的環境下都能夠表現出這兩種性質。量子力學認為自然界所有的粒子,如光子、電子或是原子,都能用一個微分方程式,如薛丁格方程式來描述。這個方程式的解即為波函數,它描述了粒子的狀態。波函數具有疊加性,即,它們能夠像波一樣互相干涉和繞射。同時,波函數也被解釋為描述粒子出現在特定位置的機率幅。這樣,粒子性和波動性就統一在同一個解釋中。
之所以在日常生活中觀察不到物體的波動性,是因為他們皆質量太大,導致德布羅意波長比可觀察的限度要小很多,因此可能發生波動性質的尺度在日常生活經驗範圍之外。這也是為什麼古典力學能夠令人滿意地解釋「自然現象」。反之,對於基本粒子來說,它們的質量和尺度決定了它們的行為主要是由量子力學所描述的,因而與我們所習慣的圖景相差甚遠。
[编辑] 惠更斯和牛頓,早期光理論
最早的綜合光理論是由克里斯蒂安·惠更斯所發展的,他提出了一個光的波動理論,解釋了光波如何形成波前,直線傳播。該理論也能很好地解釋折射現象。但是,該理論在另一些方面遇見了困難。因而它很快就被艾薩克·牛頓的粒子理論所超越。牛頓認為光是由微小粒子所組成,這樣他能夠很自然地解釋反射現象。並且,他也能稍顯麻煩地解釋透鏡的折射現象,以及通過三稜鏡將陽光分解為彩虹。
由於牛頓無與倫比的學術地位,他的理論在一個多世紀內無人敢於挑戰,而惠更斯的理論則漸漸為人淡忘。直到十九世紀初繞射現象被發現,光的波動理論才重新得到承認。而光的波動性與粒子性的爭論從未平息。
[编辑] 費涅爾、馬克士威和楊
十九世紀早期由托馬斯·楊和奧古斯丁·簡·菲涅耳所演示的雙狹縫實驗為惠更斯的理論提供了實驗依據:這些實驗顯示,當光穿過網格時,可以觀察到一個干涉樣式,與水波的干涉行為十分相似。並且,通過這些樣式可以計算出光的波長。詹姆斯·克拉克·馬克士威在世紀末葉給出了一組方程式,揭示了電磁波的性質。而方程式得到的結果,電磁波的傳播速度就是光速,這使得光作為電磁波的解釋被人廣泛接受,而惠更斯的理論也得到了重新認可。
[编辑] 愛因斯坦和光子
1905年,愛因斯坦對光電效應提出了一個理論,解決了之前光的波動理論所無法解釋的這個實驗現象。他引入了光子,一個攜帶光能的量子的概念。
在光電效應中,人們觀察到將一束光線照射在某些金屬上會在電路中產生一定的電流。可以推斷是光將金屬中的電子打出,使得它們流動。然而,人們同時觀察到,對於某些材料,即使一束微弱的藍光也能產生電流,但是無論多麼強的紅光都無法在其中引出電流。根據波動理論,光強對應於它所攜帶的能量,因而強光一定能提供更強的能量將電子擊出。然而事實與預期的恰巧相反。
愛因斯坦將其解釋為量子化效應:電子被光子擊出金屬,每一個光子都帶有一部分能量E,這份能量對應於光的頻率ν:

這裡h是普朗克常數(6.626 x 10-34 J s)。光束的顏色決定於光子的頻率,而光強則決定於光子的數量。由於量子化效應,每個電子只能整份地接受光子的能量,因此,只有高頻率的光子(藍光,而非紅光)才有能力將電子擊出。
愛因斯坦因為他的光電效應理論獲得了1921年諾貝爾物理學獎。
[编辑] 德布羅意
1924年,路易·德布羅意構造了德布羅意假說,聲稱所有的物質都有類波的屬性。他將這個波長λ和動量p聯繫為:

這是對愛因斯坦等式的一般化,因為光子的動量為p = E / c(c為真空中的光速),而λ = c / ν。
德布羅意的方程式三年後通過兩個獨立的電子散射實驗被證實於電子(具有靜止質量)身上。在阿伯丁大學,喬治·佩吉特·湯姆森將一束電子穿過薄金屬片,並且觀察到了預期中的干涉樣式。在貝爾實驗室,柯林頓·戴維森和雷斯特·革末將他們的實驗電子束穿過一個晶體。
德布羅意於1929年因為這個假設獲得了諾貝爾物理學獎。湯姆森和戴維森因為他們的實驗工作共享了1937年諾貝爾物理學獎。
[编辑] 外部連結