维基百科，自由的百科全书

反物質

大綱

湮滅

裝置

粒子加速器

潘寧阱

反粒子

正電子

反質子

反中子

反μ子

反τ子

反電子中微子

反μ子中微子

反τ子中微子

用途

正子斷層掃描

反物質燃料

反物質武器

機構

ALPHA Collaboration

ATHENA

ATRAP

CERN

KEK (BELLE)

SLAC (BaBar)

IHEP

名人

保羅·狄拉克

趙忠堯

卡爾·安德森

編輯

湮滅（英語：annihilation）是指當物質和它的反物質相遇時，會發生完全的物質-能量轉換，產生能量（如以光子的形式）的過程，又稱互毀、相消、對消滅。

其遵守愛因斯坦的質能守恆定律E=mc²。其中E為湮滅產生能量，m為物質湮滅前總質量，c為光速≈3x10⁸米/秒。舉例來說，二分之一克反物質湮滅所產生的能量和廣島市原子彈爆炸所產生的能量相當(即是一克反物質湮滅所產生的能量約為20-30千噸 TNT當量，或者是大約200萬千卡)。

一個正電子和一個電子碰撞後湮滅，通過光子的形式釋放能量，這一過程仍然滿足電荷守恆定律，因為湮滅前後宇宙的電荷總和保持為0。

這是一篇與粒子物理學相關的小作品，你可以透過編輯或修訂擴充其內容。

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

2个分类:

粒子物理學

反物質

無窮

维基百科，自由的百科全书

（重定向自∞）

此條目列出了一些參考來源或外部連結，但由於缺少內文腳註，條目中部分資訊的來源仍然不明確。（2011年5月15日）
請通過加入合適的內文腳註來改善這篇條目。

數學的數

基本

$\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}\sub\mathbb{R}\sub\mathbb{C}$

自然數 $\mathbb{N}$
整數 $\mathbb{Z}$
二進分數
 有限小數
 循環小數
 有理數 $\mathbb{Q}$
高斯整數 $\mathbb{Z}[i]$
代數數 $\mathbb{A}$
實數 $\mathbb{R}$
複數 $\mathbb{C}$

負數
 分數
 單位分數
 無限小數
 規矩數
 無理數
 超越數
 二次無理數
 虛數
 艾森斯坦整數 $\mathbb{Z}[\omega]$

延伸

雙複數
 四元數 $\mathbb{H}$
共四元數
 八元數 $\mathbb{O}$
超數
 上超實數
 超現實數

超複數
 十六元數 $\mathbb{S}$
複四元數
 Tessarine
大實數
 超實數 ${}^\star\mathbb{R}$

其他

對偶數
 雙曲複數
 序數
 質數
 同餘
 可計算數
 艾禮富數

公稱值
 超限數
 基數
 P進數
 規矩數
 整數序列
 數學常數

圓周率 π = 3.141592653…
自然對數的底 e = 2.718281828…
虛數單位 i = $+\sqrt{-1}$
無窮大量 ∞

無窮或無限，數學符號為∞。來自於拉丁文的「infinitas」，即「沒有邊界」的意思。它在神學、哲學、數學和日常生活中有著不同的概念。通常使用這個詞的時候並不涉及它的更加技術層面的定義。
在神學方面，例如在像神學家東斯歌德（Duns Scotus）的著作中，上帝的無限能量是運用在無約束上，而不是運用在無限量上。在哲學方面，無窮可以歸因於空間和時間。在神學和哲學兩方面，無窮又作為無限，很多文章都探討過無限、絕對、上帝和芝諾悖論等的問題。
在數學方面，無窮與下述的主題或概念相關：數學的極限、阿列夫數、集合論中的類、戴德金－無限群、羅素悖論、超實數、射影幾何、擴展的實數軸以及絕對無限。在一些主題或概念中，無窮被認為是一個超越邊界而增加的概念，而不是一個數。
在大眾文化方面，《玩具總動員》中巴斯光年的口頭禪：「To infinity and beyond!」（到達無窮，超越無窮），這句話也可被看作研究大型基數的集合論者的吶喊。

[编辑] 歷史

[编辑] 早期無限的觀點

最早關於無限的記載出現在印度的夜柔吠陀（公元前1200－900）。書中說：「如果你從無限中移走或添加一部分，剩下的還是無限。」

印度耆那教的經書《Surya Prajnapti》(c. 400 BC) 把數分作三類：「可計的」、「不可計的」及「無限」。每一類再細分作三序分：

可計的:小的、中的與大的。

不可計的: 接近不可計的、真正不可計的與計無可計的。

無限：接近無限、真正無限與無窮無盡。

現代科學家解析古代羊皮卷中的阿基米德手稿，在殘卷《方法》命題14中，發現阿基米德開始計算無窮大的數目。他採取近似於19世紀微積分與集合論的手法，計算了兩組無窮大的集合，以求和的方法，證明它們之間的數目是相等的。

這是在人類記載上第一次出現無限也可以分類這一個念頭。

[编辑] 文藝復興時代至近代

伽利略最先發現一個集合跟它自己的正適子集可以有相同的大小。

他用上一一對應的概念說明自然數集{1, 2, 3, 4 ...}跟子集平方數集{1,4,9,16,...}一樣多。就是1→1、2→4、3→9、4→16、.....

一一對應正是用於研究無限必要的手法。

[编辑] 神學中的無窮

我們眼中的無限在上帝眼中都為有限，我們無法理解上帝的無限，因為我們不被允許跨越過上帝的知識範圍。

[编辑] 數學中的無窮

對於無限有以下解釋或定義

「無限不是指邊界外就沒有東西，而是指邊界外永遠有另一個邊界存在。」

[编辑] 實分析中的無窮

在實分析中，符號 $\infty$ 稱為「無窮」，代表無界極限。 $x \to \infty$ 表示 $x \quad$ 超出任意給定值， $x \to -\infty$ 表示 $x \quad$ 最終小於任意給定值。標記為 $\infty$ 和 $-\infty$ 的點加入到實數組成的拓撲空間，就產生實數集的「兩點緊緻化」。再加入代數屬性，我們就得到了超實數。也可將 $\infty$ 和 $-\infty$ 作為一個點，並得到實數的「一點緊緻化」，也就是實射影線。射影幾何在平面幾何上引入無窮遠線，在高維上也有類似概念。

[编辑] 無窮大和無窮小

一般講無窮指的都是無窮大，但是無窮小也是一種無窮。通過 $y = 1 / x$ 的映射即可把無窮大映射為無窮小。在微積分中，常用高階無窮小的概念。

[编辑] 無窮遠點

無窮遠點是一個加在實數軸上後得到實射影直線 $\mathbb{R}P^1$ 的點。

[编辑] 集合論中的無窮

在集合論中對無窮有不同的定義。德國數學家康托爾提出，對應於不同無窮集合的元素的個數（基數），有不同的「無窮」。

這裡比較不同的無窮的「大小」的時候唯一的辦法就是通過是否可以建立「一一對應關係」來判斷，而拋棄了歐幾里得「整體大於部分」的看法。例如整數集和自然數集由於可以建立一一對應的關係，它們就具有相同的無窮基數。

例如，

可數集合，如自然數集，整數集乃至有理數集對應的基數被定義為阿列夫0（ $\aleph_0$ ）。

比可數集合「大」的稱之為不可數集合，如實數集，其基數與自然數的冪集相同（ $2^{\aleph_0}$ ）。

由於一個無窮集合的冪集總是具有比它本身更高的基數，所以通過構造一系列的冪集，可以證明無窮的基數的個數是無窮的。然而有趣的是，無窮基數的個數比任何基數都多，從而它是一個比任何無窮大都要大的「無窮大」，它不能對應於一個基數，否則會產生康托爾悖論的一種形式。

[编辑] 無窮的虛數形式標記

無窮是自然科學理論及現象描述中的重要概念及思想，當取

$s = \arctan \left( i \right)$ ， $i^2 = -1 \quad$

時，通過Euler公式可得

$-i \times \tanh(i \cdot s) = \tan(s) = i$ ，

$\exp(i \cdot s) = 0$ 。

這表明 $is \quad$ 是對負無窮大（ $- \infty$ ）予以虛數形式的標記^[1]。

[编辑] 無窮影象

被普遍認為的「兩塊鏡子產生無窮影象」實際上是錯的。首先，在物理學界，光的速度是有限的（約每秒 300,000,000 米），鏡子上我們能看到的影象是因為光在鏡子上反射才會出現。可是，光的速度有限，因此兩塊鏡子產生的影象亦會有限，而且影象的數目會以一直變慢的增長率增加。

[编辑] 參考條目

0.999…

非標準分析

連續統假設

無限猴子定理

無窮公理

銜尾蛇

[编辑] 參考文獻

^ YAN Kun. Primary annotation of symbol basing on imaginary form about infinity(R).Xi'an Modern Nonlinear Science Applying Institute, 18 March 2009.

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

4个分类:

集合論

哲學理論

神學

無窮

虛數

维基百科，自由的百科全书

（重定向自虛數）

數學的數

基本

$\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}\sub\mathbb{R}\sub\mathbb{C}$

自然數 $\mathbb{N}$
整數 $\mathbb{Z}$
二進分數
 有限小數
 循環小數
 有理數 $\mathbb{Q}$
高斯整數 $\mathbb{Z}[i]$
代數數 $\mathbb{A}$
實數 $\mathbb{R}$
複數 $\mathbb{C}$

負數
 分數
 單位分數
 無限小數
 規矩數
 無理數
 超越數
 二次無理數
虛數
艾森斯坦整數 $\mathbb{Z}[\omega]$

延伸

雙複數
 四元數 $\mathbb{H}$
共四元數
 八元數 $\mathbb{O}$
超數
 上超實數
 超現實數

超複數
 十六元數 $\mathbb{S}$
複四元數
 Tessarine
大實數
 超實數 ${}^\star\mathbb{R}$

其他

對偶數
 雙曲複數
 序數
 質數
 同餘
 可計算數
 艾禮富數

公稱值
 超限數
 基數
 P進數
 規矩數
 整數序列
 數學常數

圓周率 π = 3.141592653…
自然對數的底 e = 2.718281828…
虛數單位 i = $+\sqrt{-1}$
無窮大量 ∞

在數學裡，如果有數平方是負數的話，那個數就是虛數了；所有的虛數都是複數。「虛數」這個名詞是17世紀著名數學家笛卡爾創製，因為當時的觀念認為這是真實不存在的數字。後來發現虛數可對應平面上的縱軸，與對應平面上橫軸的實數同樣真實。虛數軸和實數軸構成的平面稱複數平面，複平面上每一點對應著一個複數。

每一個虛數可表達為 $ib\,$ ，其中 $b\,$ 是實數，虛數單位 $i\,$ 的定義是：

$i^2 = -1\,$

或者 $i = \sqrt{-1}\,$

$i = \sqrt{-1}\,$ 往往被誤認為是錯的，他們的證明的方法是：

$-1\,=i \times i=\sqrt{-1} \times \sqrt{-1}=\sqrt{-1 \times -1}=\sqrt{1}=1\,$ ， $-1\ne1\,$ 。

但請注意： $\sqrt{a \times b}=\sqrt{a} \times \sqrt{b}\,$ 成立的條件有a,b不能同時為負數。^[1]

我們應該將根號視為求 $x 2$ 的解，故將一個數開根號後會有兩個合理的值，此二值互相差一個負號。在將正數開根號時，這兩個值一為正數一為負數，故習慣上直接將根號對應到正值，而負值的解以根號前加負號來表示。但對其它的數而言開根號沒有自然的對應， $\sqrt{-1}$ 實際上代表的是兩個數，分別為 $+ i$ 及 $- i$ 。但若直接將 $\sqrt{-1}$ 對應到 $+ i$ ，而 $-\sqrt{-1}$ 對應到 $- i$ 也未嘗不可。

$i$ 稱為虛數單位。在電子學及相關領域內， $i$ 通常表達電流，故改為以 $j$ 表示虛數單位。每個複數可唯一地寫成一個實數及一個虛數的和。

$i$ 的高次方會不斷作以下的循環：

$i^0 = 1\,$

$i^1 = i\,$

$i^2 = -1\,$

$i^3 = -i\,$

$i^4 = 1\,$

$i^5 = i\,$

$i^6 = -1\,$

$i^7 = -i\,$

...

^[2]

由於虛數特殊的運算規則，出現了下列算式

$i^1 + i^2 + i^3 + i^4 =0\,$

這也暗示了 $i\,$ 為方程 $x+x^2+x^3+x^4 = 0\,$ 的根，另三個根分別為 $-i , -1\,$ 及 $0\,$ 。

由於虛數特殊的運算規則，出現了符號

$\omega^2 + \omega + 1 = 0\,$

$\omega^3 = 1\,$ 的簡式。

如果再將這個概念擴展開去，就可以組成四元數（Quaternion）、八元數（Octonion）等特殊數學範疇。

而不同的虛數都是不能比較大小的：

$1<2\,$ 成立，但 $1+i<2+i\,$ 和 $i<2i\,$ 卻均不成立。

[编辑] 視頻講解（英文）

虛數i的介紹

$i^{7321}\,$ 的計算方法舉例

i作為-1的平方根

[编辑] 參考

^ i作為-1的平方根（英文）

^ $i^{7321}\,$ 的計算方法舉例（英文視頻）

[编辑] 參看

四元數

八元數

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

複數

閔考斯基時空

维基百科，自由的百科全书

（重定向自類時）

汉漢▼

阿爾伯特·愛因斯坦在瑞士蘇黎世聯邦科技大學時期的數學老師赫爾曼·閔可夫斯基在愛因斯坦提出狹義相對論之後，於1907年將愛因斯坦與亨德里克·勞侖茲的理論結果重新表述成(3+1)維的時空，其中光速在各個慣性參考系皆為定值，這樣的時空即以其為名，稱為閔可夫斯基時空，或稱閔可夫斯基空間。

愛因斯坦一開始不認為這樣的表述有何重要性，但當他1907年開始轉往廣義相對論發展時，發現閔可夫斯基時空可說是其所要發展的理論架構的基礎，轉而對這樣的表述採取高的評價。

[编辑] 標準基底

閔可夫斯基時空的一組常用標準基底是四個互相正交的向量的集合(e₀, e₁, e₂, e₃) 使得

$-\left(e_0\right)^2 = (e_1)^2 = (e_2)^2 = (e_3)^2 = 1$

這些條件可以更簡要地寫成如下形式：

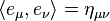
$\langle e_\mu, e_\nu \rangle = \eta_{\mu\nu}$

其中μ與ν涵蓋的數值有{0, 1, 2, 3}，矩陣η稱為閔可夫斯基度規，數值為

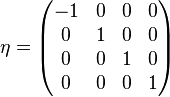
$\eta = \begin{pmatrix} -1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1 \end{pmatrix}$

相對於一組標準基底，一向量 $V$ 的分量可以寫作 $(V 0, V 1, V 2, V 3)$ ，並且我們使用愛因斯坦標記來寫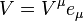 $V = V^\mu e_\mu\,$ 。分量 $V 0$ 稱作 $V$ 的「類時分量」(timelike component)，而其他三個分量則稱作「類空分量」(spatial components)。

以分量來寫，兩個向量 $V$ 與 $W$ 間的內積可寫成

$\langle V,W\rangle = \eta_{\mu\nu}V^\mu W^\nu = -V^0W^0 + V^1W^1 + V^2W^2 + V^3W^3$ ，

而一向量 $V$ 的範數(norm)平方值為

$V^2 = \eta_{\mu\nu}V^\mu V^\nu = -(V^0)^2+(V^1)^2+(V^2)^2+(V^3)^2\,$ 。

[编辑] 因果結構

四維向量依據它們（閔可夫斯基）內積的正負號來區分。四維向量 $U$ 、 $V$ 與 $W$ 可分類如下：

$V$ 是類時(timelike)，若且唯若 $\eta_{\mu \nu}V^\mu V^\nu \, = V^\mu V_\mu < 0$

$U$ 是類空(spacelike)，若且唯若 $\eta_{\mu \nu }U^\mu U^\nu \, = U^\mu U_\mu > 0$

$W$ 是零(null)或稱類光(lightlike)，若且唯若 $\eta_{\mu \nu}W^\mu W^\nu \, =W^\mu W_\mu = 0$

這樣的術語源自於相對論中對於閔可夫斯基時空的使用。閔可夫斯基時空中一事件所有零向量的集合構成了該事件的光錐(light cone)。注意到這些標記的使用與參考系無關。

向量場被稱作是類時、類空或零，是看場定義所在的各點，其所對應的向量是類時、類空或零。

關於零向量一個有用的結果：「若兩個零向量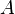 $A\,$ 、 $B\,$ 正交（即：零內積值 $A\cdot B = A^\mu B_\mu = 0$ ），則它們必定是呈比例關係 $A=kB\,$ （ $k\,$ 為常數）。」

一旦時間方向選定了，類時向量與零向量可以再分為各種類別。以類時向量(timelike vector)來說，我們有

未來方向(future directed)類時向量，其第一個分量為正，而

過去方向(past directed)類時向量，其第一個分量為負。

以零向量(null vector)來說，可分為三種類別：

純零向量(zero vector)，其在任何基底下，所有分量皆為(0,0,0,0)。

未來方向零向量，其第一個分量為正，而其餘分量為0。

過去方向零向量，其第一個分量為負，而其餘分量為0。

加上類空向量，全部共有六種類別。

閔可夫斯基時空中的正交歸一基底(orthonormal basis)必然包含一個類時與三個類空的單位向量。若希望以非正交歸一基底來做運算，則可有其他的向量組合。例如：可以輕鬆建構一種（非正交歸一）基底，整個是由零向量所組成，稱之為「零基底」(null basis)。

[编辑] 誤解

由於閔可夫斯基時空的緣故，許多人常聽到『「空間」與時間可以組成一個四維【空間】』這樣的句子，因而誤以為時間跟空間是等價的，但事實上相對論只描述了空間跟時間有著互相影響的特性，時間並沒有像空間一般可以自由移動的特性。上面那個句子中第一個「空間」指的是一般的空間無誤，但第二個【空間】指的其實是閔可夫斯基時空，是數學上的【空間】，而非物理上的「空間」。

[编辑] 相關條目

歐幾里得空間

時空

光速

世界線

狹義相對論

勞侖茲流形

雙曲空間

雙曲四元數

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

6个分类:

狹義相對論

廣義相對論的精確解

幾何學

量子場論

閔可夫斯基時空

洛倫茲流形

封閉類時曲線

维基百科，自由的百科全书

汉漢▼

在一勞侖茲流形中，一條封閉類時曲線（closed timelike curve, CTC）是一物質粒子於時空中的一種世界線，其為「封閉」，亦即會返回起始點。這種可能性是由Willem Jacob van Stockum於1937年以及庫爾特·哥德爾（Kurt Gödel）於1949年開啟研究風潮。若CTC存在，則似乎隱射時間機器理論上可行，如此也引出了祖父悖論（grandfather paradox）的夢靨。CTC與參考系拖曳（frame dragging）以及提普勒柱體（Tipler Cylinder）有關。這是廣義相對論帶來的眾多有趣的「副作用」其中一者。

[编辑] 光錐

下方光錐是平直時空中典型的光錐模樣——所有包含在光錐裡的時空座標具有較遲的時間. 上方光錐不僅是於同時間點包含了其他空間位置，它也不包含未來時間的x=0，而包含了早先的時間。

當在廣義相對論中討論一系統的演進，或將討論限定在閔可夫斯基時空，物理學家常提及「光錐」。一個光錐表示一給定現在狀態的物體未來任何可能的演進，或給定現在位置之下，未來任何可能的位置。一個物體的未來可能位置受限於該物體能移動的速度，最快只能到光速。舉例而言，一個物體於時間 $t 0$ 位於位置 $p$ ，於時間 $t 1$ 時，僅能移動到 $c (t 1 - t 0)$ 之內的位置。

[编辑] 廣義相對論

CTC有著令人難安的習性：會出現在廣義相對論的核心——愛因斯坦場方程式所得「局域上」無可異議的精確解，其為幾個最重要解中的數個。包括有：

克爾真空(Kerr vacuum)（此為不帶電荷、磁荷且旋轉之黑洞的模型）

van Stockum塵（此為具有柱狀對稱結構之宇宙塵的模型）

哥德爾Λ塵(Gödel lambdadust)（此為慎選宇宙常數項Λ下宇宙塵的模形）

J. Richard Gott提出了利用宇宙弦製造CTC的機制。

這些例子中的幾個如同提普勒柱體，相當斧鑿而不自然，但克爾解的「外面」部份則被認為某種程度上是一般性的，所以一旦得知其「內部」含有CTC，則令人相當不安。多數物理學家感覺這樣的解中的CTC是人為客體(artifact)。

[编辑] 相關條目

類時

廣義相對論

[编辑] 參考文獻

S. Carroll. Spacetime and Geometry. Addison Wesley. 2004. ISBN 0-8053-8732-3.

Kurt Gödel. An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation. Rev. Mod. Phys.. 1949, 21: 447.

[编辑] 外部連結

A Primer on Time Travel -(backup in the Internet Archive)

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

3个分类:

時間旅行

勞侖茲流形

相對論

中文數字

维基百科，自由的百科全书

注意：本頁面或章節含有Unicode中日韓統一表意文字擴展A區用字：「䦉」。如果您的系統不支援，有關字元將會錯誤顯示成空格、問號或者方格等。參見維基百科:Unicode擴展漢字。

此條目沒有列出任何參考或來源。（2007年8月）
維基百科所有的內容都應該可供查證。
請協助添加來自可靠來源的引用以改善這篇條目。無法查證的內容可能被提出異議而移除。

記數系統
印度-阿拉伯數字系統
西方阿拉伯數字阿拉伯文數字高棉數字	印度數字波羅米數字泰語數字
漢字文化圈記數系統
中文數字越南語數字算籌	日語數字韓文數字蘇州碼子
字母記數系統
阿拉伯字母數字亞美尼亞數字西里爾數字吉茲數字	希伯來數字希臘數字阿利耶波多數字
其它記數系統
雅典數字巴比倫數字埃及數字伊特拉斯坎數字	瑪雅數字羅馬數字
依底數區分的進位制系統
十進制 (10)
1 2 3 4 5 6 7 8 9 12 16 20 60
進位制系統列表
查 · 論 · 編

中文數字，是中文使用的數字系統，在阿拉伯數字傳入前廣泛使用。目前在計算中漸少使用。東亞地區書寫支票時仍會使用中文數字（通常是「大寫」），因筆劃繁複較難做假。

[编辑] 一般數字

中文有九個字代表「一」至「九」，另有其他數字代表「十」、「百」、「千」等較大數。

每個數字都有大、小兩種寫法。大寫常見於正式或商業文件之上，以避免被塗改。

拼音	注音	大寫	小寫	數值	備註
líng	ㄌㄧㄥˊ	零	〇	0	在軍事、航空無線電通信或鐵路上讀作「洞」。〇是標準的表示方式^[1]，零有時也可以接受。
yī	ㄧ	壹	一	1	在軍事、航空無線電通信或鐵路上讀作「幺」（yāo），在中國讀出號碼的時候亦常用。舊時大寫也作弌。
èr	ㄦˋ	貳	二	2	在軍事、航空無線電通信或鐵路上讀作「兩」。舊時大寫也作弍。作兩時用於千、萬位或之前及量詞之前。但重量「二両」不作「兩両」。
sān	ㄙㄢ	參	三	3	又作叄。舊時大寫也作弎。
sì	ㄙˋ	肆	四	4	在軍事、航空無線電通信或鐵路上讀作「刀」。舊時大寫也作䦉。
wǔ	ㄨˇ	伍	五	5
liù	ㄌㄧㄡˋ	陸	六	6
qī	ㄑㄧ	柒	七	7	在軍事、航空無線電通信或鐵路上讀作「拐」。
bā	ㄅㄚ	捌	八	8
jiǔ	ㄐㄧㄡˇ	玖	九	9	在軍事、航空無線電通信或鐵路上讀作「勾」。
shí	ㄕˊ	拾	十	10	雖然有些人會用什（讀作shí）表示，但是這是容易被塗改成「仟」的。
niàn	ㄋㄧㄢˋ	念	廿	20	或做卄。今仍多以二十表示，但日曆中的農曆和台灣報紙仍慣用廿來記載日期，多訓讀作「二十」。粵語中多以「廿」代替「二十」。大寫的念戰後已不見使用，今多以貳拾表示。右圖是一枚1931年中華民國郵政發行的「念圓」（2000）郵票。
sà	ㄙㄚˋ	叁拾	卅	30	今仍多以三十表示，但日曆中的農曆和台灣報紙仍慣用卅來記載日期，多訓讀作「三十」。粵語中多以「卅」代替「三十」。
xì	ㄒㄧˋ	肆拾	卌	40	罕以卌（讀作「系」）表示。常以四十表示。不像廿和卅，粵語不以「卌」代替「四十」。
bǎi	ㄅㄞˇ	佰	百	100
bì	ㄅㄧˋ	貳佰	皕	200	罕以皕（讀作「必」）表示。常以二百表示。
qiān	ㄑㄧㄢ	仟	千	1,000
wàn	ㄨㄢˋ	萬	萬	10⁴	中國數字以10⁴為組。
yì	一ˋ	億	億	10⁸	在古代，億也可代表10⁵。詳看大數系統。亦作萬萬，例如馬關條約中「平銀貳萬萬兩交與日本，作為賠償軍費」。
zhào	ㄓㄠˋ	兆	兆	10¹²	在古代，兆也可代表10⁶、10¹⁶。因為兆也可以表示「百萬」，造成其用法爭議，請看國際單位制詞頭。
jīng	ㄐㄧㄥ	京	京	10¹⁶	在古代，京也可代表10⁷、10²⁴、10³²。也作經。
gāi	ㄍㄞ	垓	垓	10²⁰	在古代，垓也可代表10⁸、10³²、10⁶⁴。
zǐ	ㄗˇ	秭	秭	10²⁴	在古代，秭也可代表10⁹、10⁴⁰、10¹²⁸。也作杼。佑才是對應的國際單位制詞頭。
ráng	ㄖㄤˊ	穰	穰	10²⁸	在古代，穰也可代表10¹⁰、10⁴⁸、10²⁵⁶。也作壤。
gōu	ㄍㄡ	溝	溝	10³²	在古代，溝也可代表10¹¹、10⁵⁶、10⁵¹²。
jiàn	ㄐㄧㄢˋ	澗	澗	10³⁶	在古代，澗也可代表10¹²、10⁶⁴、10¹⁰²⁴。
zhèng	ㄓㄥˋ	正	正	10⁴⁰	在古代，正也可代表10¹³、10⁷²、10²⁰⁴⁸。
zài	ㄗㄞˋ	載	載	10⁴⁴	在古代，載也可代表10¹⁴、10⁸⁰、10⁴⁰⁹⁶。

以「一」開首的數字有時可省略「一」，只限於後接「十」時。非正式場合，「百」、「千」、「萬」都可省略「一」，如「千三」即為「1300」。

個位以前的「0」要寫或讀出來，但連續的0隻要寫或讀一個便可。例如：10002 應寫成「一萬零二」。

若末位前不是「零」字，則末位之單位可省略。如「一萬二」是12000的簡稱。

「載」以上尚有萬進單位「極」（10⁴⁸）、「恆河沙」（10⁵²或10⁵⁶）、「阿僧祇」（10⁵⁶或10⁶⁴）、「那由他」（10⁶⁰或10⁷²）、「不可思議」（10⁶⁴或10⁸⁰）、「無量大數」（10⁶⁸或10⁸⁸），至今已絕少有人使用。

拼音	注音	大寫	數值	備註
fēn	ㄈㄣ	分	10^-1	也是對應的國際單位詞頭。
lí	ㄌ一ˊ	厘	10^-2	也作釐。也是對應的國際單位詞頭。
háo	ㄏㄠˊ	毫	10^-3	也作毛。也是對應的國際單位詞頭。
sī	ㄙ	絲	10^-4	古代中文數字。
hū	ㄏㄨ	忽	10^-5	古代中文數字。
wēi	ㄨㄟˊ	微	10^-6	也是對應的國際單位詞頭。
xiān	ㄒㄧㄢ	纖	10^-7	古代中文數字。
shā	ㄕㄚ	沙	10^-8	古代中文數字。
chén	ㄔㄣˊ	塵	10^-9	古代中文數字。奈才是對應的國際單位詞頭。
āi	ㄞ	埃	10^-10	古代中文數字。
miǎo	ㄇㄧㄠˇ	渺	10^-11	古代中文數字。
mò	ㄇㄛˋ	漠	10^-12	古代中文數字。皮才是對應的國際單位詞頭。
móhu	ㄇㄛˊㄏㄨˊ	模糊	10^-13	古代中文數字。
qūnxún	ㄑㄩㄣㄒㄩㄣˊ	逡巡	10^-14	古代中文數字。
xūyú	ㄒㄩㄩˊ	須臾	10^-15	古代中文數字。
shùnxī	ㄕㄨㄣˋㄒㄧ	瞬息	10^-16	古代中文數字。
tánzhǐ	ㄊㄢˊㄓˇ	彈指	10^-17	古代中文數字。
chànà	ㄔㄚˋㄋㄨㄛˊ	剎那	10^-18	古代中文數字。
lìudé	ㄌㄧㄡˋㄉㄜˊ	六德	10^-19	古代中文數字。
xūkōng	ㄒㄩㄎㄨㄥ	虛空	10^-20	古代中文數字。
qīngjìng	ㄑㄧㄥㄐㄧㄥˋ	清靜	10^-21	古代中文數字。

[编辑] 對周邊國家的影響

種類	數值	大寫	小寫	漢語				朝鮮語		越南語		日語
				中古音^[2]	普通話／國語	上海話	廣東話	漢字詞	固有詞	漢字詞（漢越詞）	固有詞（純越詞）	漢字詞（音讀）		固有詞（訓讀）
				中古音^[2]	普通話／國語	上海話	廣東話	漢字詞	固有詞	漢字詞（漢越詞）	固有詞（純越詞）	漢音	吳音	固有詞（訓讀）
數字	0	零	〇	leng^[3]	líng／ㄌㄧㄥˊ	lin	ling⁴	영(yeong) · 령(ryeong)^[4] 【「空／공(gong)」也常用來表記「0」】	【無】	linh 【「空／không」也常用來表記「0」】	【無】	れい（rei）	りょう（ryō）	【無】
	1	壹	一	ʔjit	yī／ㄧ	yih	yat¹	일(il)	하나(hana)	nhất	một／𠬠	いつ（itsu）	いち（ichi）	ひと（hito）
	2	貳	二	nyijH	èr／ㄦˋ	nyi	yi⁶	이(i)	둘(dul)	nhị	hai／𠄩	じ（ji）	に（ni）	ふた（futa）
	3	參	三	sam	sān／ㄙㄢ	se	saam¹	삼(sam)	셋(set)	tam	ba／𠀧	さん（san）	さん（san）	み（mi）
	4	肆	四	sijH	sì／ㄙˋ	si	sei³	사(sa)	넷(net)	tứ	bốn／𦊚	し（shi）	し（shi）	よ（yo） · よん（yon）
	5	伍	五	nguX	wǔ／ㄨˇ	ng	ng⁵	오(o)	다섯(daseot)	ngũ	năm／𠄼	ご（go）	ご（go）	いつ（itsu） · い（i）
	6	陸	六	ljuwk	liù／ㄌㄧㄡˋ	loh	luk⁶	육(yuk) · 륙(ryuk)^[5]	여섯(yeoseot)	lục	sáu／𦒹	りく（riku）	ろく（roku）	む（mu）
	7	柒	七	tshit	qī／ㄑㄧ	chieh	chat¹	칠(chil)	일곱(ilgop)	thất	bảy／𦉱	しつ（shitsu）	しち（shichi）	なな（nana）
	8	捌	八	pɛt	bā／ㄅㄚ	pah	baat³	팔(pal)	여덟(yeodeol)	bát	tám／𠔭	はつ（hatsu）	はち（hachi）	や（ya）
	9	玖	九	kjuwX	jiǔ／ㄐㄧㄡˇ	jioe	gau²	구(gu)	아홉(ahop)	cửu	chín／𠃩	きゅう（きう）（kyū (kiu)）	く（ku）	ここの（kokono）
位	10	拾	十	dzyip	shí／ㄕˊ	zeh	sap⁶	십(sip)	열(yeol)	thập	mười／𨒒	しゅう（しふ）（shyū (shipu)）	じゅう（じふ）（jyū (jipu)）	とお（とを）（too (towo)）、そ（so）
	100	佰	百	pæk	bǎi／ㄅㄞˇ	pah	baak³	백(baek)	온(on)	bách	trăm／𤾓	はく（haku）	ひゃく（hyaku）	もも（momo）、お（ほ）（o (ho)）
	1000	仟	千	tshen	qiān／ㄑㄧㄢ	chi	chin¹	천(cheon)	즈믄(jeumeun)	thiên	nghìn (ngàn)／𠦳	せん（sen）	せん（sen）	ち（ti）
	10000	萬	萬	mjonH	wàn／ㄨㄢˋ	ve	maan⁶	만(man)	드먼(deumeon)	vạn	mười nghìn (ngàn)／𨒒𠦳	ばん（ban）	まん（man）	よろず（よろづ）（yorozu (yorodu)）
複合	20	念	廿	nyip	niàn／ㄋㄧㄢˋ	nyie	ye⁶	입(ip)	스물(seumul)	niệm	-	じゅう（じふ）（jyū (jipu)）	にゅう（にふ）（nyū (nipu)）	はた（hata）
	30	-	卅	sop	sà／ㄙㄚˋ		sa¹	삽(sap)	서른(seoreun)	tạp	-	そう（さふ）（sō (sapu)）	そう（そふ）（sō (sopu)）	みそ（miso）
	40	-	卌		xì／ㄒㄧˊ		se³	십(sip)	마흔(maheun)	tấp	-	しゅう（しふ）（shyū (shipu)）	しゅう（しふ）（shyū (shipu)）	よそ（yoso）

[编辑] 大數系統

比萬大的數字，中國傳統上使用「億、兆、京、垓、秭、穰、溝、澗、正、載」十個字來分等。但此十個字只是表示數之間大略的比較關係，並未精確指出數量級。從古自今，這十等共有四個系統。

上數、中數、下數 《五經算術》：按黃帝為法，數有十等。及其用也，乃有三焉。十等者，謂「億、兆、京、垓、秭、穰、溝、澗、正、載」也。三等者，謂「上、中、下」也。其下數者，十十變之。若言十萬曰億，十億曰兆，十兆曰京也。中數者，萬萬變之。若言萬萬曰億，萬萬億曰兆，萬萬兆曰京也。上數者，數窮則變。若言萬萬曰億，億億曰兆、兆兆曰京也。

系統	億 yì 一ˋ	兆 zhào ㄓㄠˋ	京 jīng ㄐㄧㄥ	垓 gāi ㄍㄞ	秭 zǐ ㄗˇ	穰 ráng ㄖㄤˊ	溝 gōu ㄍㄡ	澗 jiàn ㄐㄧㄢˋ	正 zhēng ㄓㄥˋ	載 zài ㄗㄞˇ	說明
下數	10⁵	10⁶	10⁷	10⁸	10⁹	10¹⁰	10¹¹	10¹²	10¹³	10¹⁴	十十變之，後者為前者十(10¹)倍。
萬進	10⁸	10¹²	10¹⁶	10²⁰	10²⁴	10²⁸	10³²	10³⁶	10⁴⁰	10⁴⁴	後者為前者萬(10⁴)倍。
中數	10⁸	10¹⁶	10²⁴	10³²	10⁴⁰	10⁴⁸	10⁵⁶	10⁶⁴	10⁷²	10⁸⁰	萬萬變之：後者為前者萬萬倍（10⁸）。
上數	10⁸	10¹⁶	10³²	10⁶⁴	10¹²⁸	10²⁵⁶	10⁵¹²	10¹⁰²⁴	10²⁰⁴⁸	10⁴⁰⁹⁶	數窮則變：不能數了才變，後者為前者之平方。

在現代中文，「萬進數」成為唯一的數字表示方式^[6]，「上、中、下數」古法已不被使用。雖然現代仍有「兆應代表何值」的爭議，但是它的用法（代表10¹²）仍然很一致的在部份中國人社區、日本、韓國等地方看見^{[來源請求]}。不過，大部份人已經不知道大於兆的數字是甚麼，就連字典對它們的定義都可能很不一致。大於載的，就是引進自天竺的佛經上的數字；而這些「佛經數字」已成為「古代用法」了。

下列是佛經數字在華嚴經內的用法：

名稱	$n$	數 $\begin{smallmatrix}(= 10^{7 \times 2^n})\end{smallmatrix}$
倶胝	0	10⁷
阿庾多	1	10¹⁴
那由他	2	10²⁸
頻波羅	3	10⁵⁶
矜羯羅	4	10¹¹²
阿伽羅	5	10²²⁴
最勝	6	10⁴⁴⁸
摩婆羅	7	10⁸⁹⁶
阿婆羅	8	10¹⁷⁹²
多婆羅	9	10³⁵⁸⁴
界分	10	10⁷¹⁶⁸
普摩	11	10¹⁴³³⁶
禰摩	12	10²⁸⁶⁷²
阿婆鈐	13	10⁵⁷³⁴⁴
彌伽婆	14	10¹¹⁴⁶⁸⁸
毘攞伽	15	10²²⁹³⁷⁶
毘伽婆	16	10⁴⁵⁸⁷⁵²
僧羯邏摩	17	10⁹¹⁷⁵⁰⁴
毘薩羅	18	10^1835008
毘贍婆	19	10^3670016
毘盛伽	20	10^7340032
毘素陀	21	10^14680064
毘婆訶	22	10^29360128
毘薄底	23	10^58720256
毘佉擔	24	10^117440512
稱量	25	10^234881024
一持	26	10^469762048
異路	27	10^939524096
顛倒	28	10^1879048192
三末耶	29	10^3758096384
毘睹羅	30	10^7516192768
奚婆羅	31	10^15032385536
伺察	32	10^30064771072
周廣	33	10^60129542144
高出	34	10^120259084288
最妙	35	10^240518168576
泥羅婆	36	10^481036337152
訶理婆	37	10^962072674304
一動	38	10^{1924145348608}
訶理蒲	39	10^{3848290697216}
訶理三	40	10^{7696581394432}
奚魯伽	41	10^{15393162788864}
達攞歩陀	42	10^{30786325577728}
訶魯那	43	10^{61572651155456}
摩魯陀	44	10^{123145302310912}
懺慕陀	45	10^{246290604621824}
瑿攞陀	46	10^{492581209243648}
摩魯摩	47	10^{985162418487296}
調伏	48	10^{1970324836974592}
離憍慢	49	10^{3940649673949184}
不動	50	10^{7881299347898368}
極量	51	10^{15762598695796736}
阿麼怛羅	52	10^{31525197391593472}
勃麼怛羅	53	10^{63050394783186944}
伽麼怛羅	54	10^{126100789566373888}
那麼怛羅	55	10^{252201579132747776}
奚麼怛羅	56	10^{504403158265495552}
鞞麼怛羅	57	10^{1008806316530991104}
鉢羅麼怛羅	58	10^{2017612633061982208}
屍婆麼怛羅	59	10^{4035225266123964416}
翳羅	60	10^{8070450532247928832}
薜羅	61	10^{16140901064495857664}
諦羅	62	10^{32281802128991715328}
偈羅	63	10^{64563604257983430656}
窣步羅	64	10^{129127208515966861312}
泥羅	65	10^{258254417031933722624}
計羅	66	10^{516508834063867445248}
細羅	67	10^{1033017668127734890496}
睥羅	68	10^{2066035336255469780992}
謎羅	69	10^{4132070672510939561984}
娑攞荼	70	10^{8264141345021879123968}
謎魯陀	71	10^{16528282690043758247936}
契魯陀	72	10^{33056565380087516495872}
摩睹羅	73	10^{66113130760175032991744}
娑母羅	74	10^{132226261520350065983488}
阿野娑	75	10^{264452523040700131966976}
迦麼羅	76	10^{528905046081400263933952}
摩伽婆	77	10^{1057810092162800527867904}
阿怛羅	78	10^{2115620184325601055735808}
醯魯耶	79	10^{4231240368651202111471616}
薜魯婆	80	10^{8462480737302404222943232}
羯羅波	81	10^{16924961474604808445886464}
訶婆婆	82	10^{33849922949209616891772928}
毘婆羅	83	10^{67699845898419233783545856}
那婆羅	84	10^{135399691796838467567091712}
摩攞羅	85	10^{270799383593676935134183424}
娑婆羅	86	10^{541598767187353870268366848}
迷攞普	87	10^{1083197534374707740536733696}
者麼羅	88	10^{2166395068749415481073467392}
駄麼羅	89	10^{4332790137498830962146934784}
鉢攞麼陀	90	10^{8665580274997661924293869568}
毘迦摩	91	10^{17331160549995323848587739136}
烏波跋多	92	10^{34662321099990647697175478272}
演説	93	10^{69324642199981295394350956544}
無盡	94	10^{138649284399962590788701913088}
出生	95	10^{277298568799925181577403826176}
無我	96	10^{554597137599850363154807652352}
阿畔多	97	10^{1109194275199700726309615304704}
青蓮華	98	10^{2218388550399401452619230609408}
鉢頭摩	99	10^{4436777100798802905238461218816}
僧祇	100	10^{8873554201597605810476922437632}
趣	101	10^{17747108403195211620953844875264}
至	102	10^{35494216806390423241907689750528}
阿僧祇	103	10^{70988433612780846483815379501056}
阿僧祇轉	104	10^{141976867225561692967630759002112}
無量	105	10^{283953734451123385935261518004224}
無量轉	106	10^{567907468902246771870523036008448}
無邊	107	10^{1135814937804493543741046072016896}
無邊轉	108	10^{2271629875608987087482092144033792}
無等	109	10^{4543259751217974174964184288067584}
無等轉	110	10^{9086519502435948349928368576135168}
不可數	111	10^{18173039004871896699856737152270336}
不可數轉	112	10^{36346078009743793399713474304540672}
不可稱	113	10^{72692156019487586799426948609081344}
不可稱轉	114	10^{145384312038975173598853897218162688}
不可思	115	10^{290768624077950347197707794436325376}
不可思轉	116	10^{581537248155900694395415588872650752}
不可量	117	10^{1163074496311801388790831177745301504}
不可量轉	118	10^{2326148992623602777581662355490603008}
不可說	119	10^{4652297985247205555163324710981206016}
不可說轉	120	10^{9304595970494411110326649421962412032}
不可說不可說	121	10^{18609191940988822220653298843924824064}
不可說不可說轉	122	10^{37218383881977644441306597687849648128}
不可說不可說不可說	123	10^{74436767763955288882613195375699296256}

[编辑] 腳註

^ Unicode U+3007；大五碼內碼：A1B3

^ Baxter, William H., An Etymological Dictionary of Common Chinese Characters. 2000 [2008-05-01]

^ 中古音，無聲調符號的表示平聲或入聲，「-X」為上聲、「-H」為去聲。

^ 「령(ryeong)」為北韓讀法。

^ 「륙(ryuk)」為北韓讀法。

^ 在中國的教科書上，規定了五位數叫做萬，十個萬叫做十萬，十個十萬為百萬，十個百萬為千萬，十個千萬為億。以此類推，有十億、百億等等計數單位。10⁴為一級，比如說有個級、萬級、億級。簡單的說，就是萬萬為一億，萬億為一兆

[编辑] 參見

十進制

國際單位制詞頭

蘇州碼子

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

2个分类:

數字

漢字

三法度論

维基百科，自由的百科全书

早期佛教

經典

巴利聖典
 阿含經
 犍陀羅佛教原稿

結集

第一次結集
 第二次結集
 第三次結集
 第四次結集

部派

最初僧伽
├ 大眾部
└ 上座部
　├ 說一切有部
　│└ 經量部
　├ 犢子部
　│└ 正量部
　└ 分別說部
　　└ 赤銅鍱部

查看 • 討論 • 編輯 • 歷史

《三法度論》是犢子部釋經的論書，東晉瞿曇僧伽提婆譯。異譯本有公元382年符秦鳩摩羅佛提等譯的《四阿鋡暮抄解》，題為婆素跋陀^[1]造。慧遠於《三法度序》稱本論為山賢造僧伽先註釋^[2]。印順稱其為犢子尊者造^[3]，呂澂稱其歸屬賢冑部^[4]。

[编辑] 篇章結構

本論以三分法為主，分三品，每品三真度（犍度），共九真度。下表以《三法度論》譯詞為主，括號中為部分《四阿鋡暮抄解》對應譯詞。

德品	福	施					第一真度
		戒
		修	禪
			無量
			無色
	根
	無惡	忍辱
		多聞
		不惡 (聖分)	真知識(善知識)
			真御意(思惟)
			真由 (得)	具 (等具)	善損 (等書)	糞掃衣
						無事
						乞食
					伏根
					近行禪
				方便	戒		第二真度
					上止 (息)	進
						念
						定
					智	見地
						修地
						無學地
				果	佛		第三真度
					辟支佛
					聲聞	離欲
						未離欲
						阿羅漢

惡品	惡行	身惡行					第四真度
		口惡行
		意惡行
	愛	染					第五真度
		恚
		慢
	無明	非智	有為不知				第六真度
			無為不知
			不可說不知
		邪智	身見
			邊見
			盜見
		惑智	寶不了
			諦不了
			定不了

依品	陰	色陰					第七真度
		行
		知	痛
			想
			識
	界	欲界					第八真度
		色界
		無色界
	入 (處)	細滑入 (更樂處)	近境界				第九真度
			不近境界
			無境界
		度入 (異學處)	一處因
			不正因
			無因
		解脫入 (解脫處)	想
			禪
			博聞

[编辑] 犢子部宗義

犢子部作為部派佛教最早的四大部派之一，在印度佛教滅亡之後，其理論只在漢譯的《三法度論》（四阿含抄解）和《三彌底部論》（依說論）中有所存留。

[编辑] 補特伽羅論

世友《異部宗輪論》記載：

「

玄奘譯《異部宗輪論》：犢子部本宗同義。謂補特伽羅非即蘊離蘊^[5]。依蘊處界假施設名^[6]。
失譯^[7]《十八部論》：彼犢子部根本見者。非即是人。亦非離。陰界入和合施設故。
真諦譯《部執異論》：可住子部是執義本。非即五陰是人。非異五陰是人。攝陰界入故。立人等假名。有三種假。一攝一切假。二攝一分假。三攝滅度假。

」

《三法度論》記載：

「

問云何不可說。答不可說者。受、過去、滅施設。……受^[8]施設者。眾生已受陰、界、入。計（眾生與陰界入是）一及餘（異）^[9]。過去施設者。因過去陰界入說。如所說「我於爾時名瞿旬陀」。滅施設者。若已滅是因受說。如所說「世尊般涅槃」。復次過去施設者。制眾生斷。滅施設者。制有常。受施設者。制無。不受施設者。制有。

」

[编辑] 補特伽羅實有論

帝須《論事》之覺音注（元亨寺譯本）記載：

「

此「補特伽羅」者，是我、有情、命者。佛教內之補特伽羅論者，仰望世尊：「為己利益之修行有補特伽羅」，而執「補特伽羅是依諦義、勝義而得」。

」

提婆設摩《識身論》記載：

「

趣補特伽羅。八種與三聚。三種^[10]自造作。見聞覺知後。補特伽羅論者^[11]作如是言。諦義勝義。補特伽羅。可得可證。現有等有。是故定有補特伽羅。

」

[编辑] 第五法藏攝我論

龍樹《大智度論》記載：

「

是佛法中亦有犢子比丘說。如四大和合有眼法。如是五眾和合有人法。犢子阿毘曇中說。五眾不離人。人不離五眾。不可說五眾是人離五眾是人。人是第五不可說法藏^[12]中所攝。^[13]

」

《三法度論》並舉三世有為、無為和不可說的記載：

「

問云何無願。答無願者。過去未來現在不樂立。無願者不立義。是入此三中過去未來現在。是一切有為。如說處經所說。彼若作是意。我及涅槃。彼不攝是三。此不應爾。所以者何。一無二義故。涅槃^[14]者離世一向無緣。彼中無意我者。離三世更無此不可說。是以三中不樂立。是謂無願。

」

「

問云何相。答相者起住壞。起者生。住者成。壞者敗。問漫說於眾生、涅槃有疑。眾生及涅槃。亦有此相。若有者為大過。即有無常。若不者此經有過。應當說起住壞是有為相。答眾生者。於相是餘不可說。若異即有常。若是即無常。是二過不可說。涅槃亦如是。是故分別當知相者。一向有為相。

」

[编辑] 阿羅漢有退論

《中阿含經·大品·福田經》記載：

「

云何九無學人。思法。昇進法。不動法。退法。不退法。護法.護則不退.不護則退。實住法。慧解脫。俱解脫。是謂九無學人。

」

《三法度論》記載：

「

阿羅漢者是說供養名。堪受供養故曰阿羅漢。問誰堪受。答為一切眾生。故說阿羅漢。是阿羅漢三種。利根鈍根中根。問云何利根。答利根者。住法升進不動法……。問云何鈍根。答鈍根者。退念護法。退法念法護法。此三是鈍根。

退法者。或差降退非聖諦故曰退法。或復於修地退。修者修習。說以不修習是名退。如學經已不數習忘。如是不修習修地退。是病業誦和諍遠行觀故退。以是故名修地。
念法者已得阿羅漢。劣行故及身劣。便作是念。我所作以作。我何為住。如是思念。思念者多品數。亦思念財產及裁衣。但此中思念。捨命護法者。不退亦不思念。但極大方便護。如貧多方便得財守。是鈍根。問中根云何。答中根者。慧解脫具不具解脫……。

」

帝須《論事》之覺音注（元亨寺譯本）記載：

「

此處有退說。言退法不退法者，依經所說「諸比丘！此二種法，導有學之比丘於退轉」，「諸比丘！此五種法，導時解脫比丘於退轉^[15]」，正量部、犢子部、說一切有部及大眾部有者許認阿羅漢之退轉。

」

[编辑] 第一義諦

《三法度論》記載：

「

問云何第一義諦。答第一義者。作字念至竟止。作字及一切念至竟止。是謂第一義諦。作者身業。字者口業。念者意業。若此三至竟滅。是謂第一義諦。是涅槃義。

」

[编辑] 二十七賢聖

《三法度論》詳細解說了《中阿含經·大品·福田經》^[16]的十八有學和九無學。

		信勝			慧勝			俱勝
未離欲^[17]	第八^[18]	從信行			從法行			俱行
	須陀洹	極七			中^[19]			家家
	薄地^[20]	一來			中^[21]			一種
離欲^[22]		信解脫^[23]			見到^[24]			身證^[25]
離欲^[22]		上流般涅槃	行般涅槃	無行般涅槃	上流般涅槃	生般涅槃	中^[26]般涅槃	行般涅槃	無行般涅槃	生般涅槃
漏盡^[27]		慧解脫^[28]^[29]^[30]			俱解脫^[31]^[30]

阿羅漢^[32]^[33]		鈍根^[15]^[29]			中根			利根
阿羅漢^[32]^[33]		退法	念法	護法^[34]	慧解脫	俱解脫^[35]		住法	升進法	不動法

[编辑] 引用

^ 《四阿鋡暮抄序》：「阿鋡暮者。秦言趣無也。阿難既出十二部經。又採撮其要逕至道法。為四阿鋡暮。與阿毘曇及律並為三藏焉。身獨學士以為至德未墜於地也。有阿羅漢。名婆素跋陀(秦言今賢人名也得無著道)。抄其膏腴以為一部。九品四十六葉。斥重去複文約義豐。真可謂經之瓔鬘也。百行美妙。辯是與非。莫不悉載也。優奧深富行之能事畢矣。有外國沙門。字因提麗。先齎詣前部國。祕之佩身。不以示人。其王彌第求得諷之。遂得布此。余以壬午之歲八月。東省先師寺廟於鄴寺。令鳩摩羅佛提執梵佛念佛護為譯。僧導曇究僧叡筆受。至冬十一月乃訖。此歲夏出阿毘曇。冬出此經。一年之中具三藏也。深以自幸。但恨八九之年。始遇斯經。恐韋編未絕不終其業耳。若加數年將無大過也。近勅譯人。直令轉梵為秦。解方言而已。經之文質所不敢易也。又有懸數懸事。皆訪其人為注其下。時復以意消息者。為其章章注修妬路者。其人註解引經本也。其有直言修妬路者。引經證非註解也。」

^ 慧遠《三法度序》：「三法度經者。蓋出四阿含。四阿含則三藏之契經。十二部之淵府也。以三法為統。以覺法為道。開而當名變而彌廣。法雖三焉。而類無不盡。覺雖一焉。而智無不周。觀諸法而會其要。辯眾流而同其原。斯乃始涉之鴻漸。舊學之華苑也。有應真大人。厥號山賢。恬思閑宇智周變通。感達識之先覺。愍後矇之未悟。故撰此三法。因而名雲。目德品暨於所依。凡三章九真度。斯其所作也。其後有大乘居士。字僧伽先。以為山賢所集雖辭旨高簡。然其文猶隱。故仍前人章句為之訓傳演散本文以廣其義顯發事類以弘其美。幽讚之功於斯乃盡。自茲而後道光於世其教行焉。於是振錫取足者。仰玄風而高。蹈禪思入微者。挹清流而洗心。高座談對之士。擬之而後言。博識淵有之賓。由之而贍聞也。有遊方沙門。出自罽賓。姓瞿曇氏。字僧伽提婆。昔在本國豫聞斯道。邪翫神趣懷佩以遊。其人雖不親承二賢之音旨。而諷味三藏之遺言。志在分德誨人不惓。每至講論嗟詠有餘。遠與同集勸令宣譯。提婆於是自執胡經。轉為晉言。雖音不曲盡而文不害意。依實去華務存其本。自昔漢興逮及有晉。道俗名賢並參懷聖典。其中弘通佛教者。傳譯甚眾。或文過其意。或理勝其辭。以此考彼殆兼先典。後來賢哲若能參通晉胡善譯方言。幸復詳其大歸以裁厥中焉。」

^ 印順《說一切有部為主的論書與論師之研究》，第九章「上座別系分別論者」，第三節「被稱為分別論者的犢子部」，第二項「三法度論與僧伽斯那」：「這部論代表犢子部的根本論義，所以我有一假設：作者婆素跋陀（度），為犢子（阿羅漢）Vātsīputra的對音，展轉傳流西域，音變而被解說為「世賢」 (Vasubhadra)。」

^ 呂澂《印度佛學源流略講》，第二講「部派佛學」，第四節「犢子系學說的要點」：「「賢冑」一名，即指世賢后代的意思。」

^ 窺基《異部宗輪論述記》：「其犢子部謂補特伽羅非即蘊離蘊。謂實有我。非有為無為。然與蘊不即不離。佛說無我。但無即蘊離蘊。如外道等所計之我。悉皆是無非無不可說。非即蘊離蘊。我既不可說。亦不可言形量大小等。乃至成佛此我常在。」

^ 窺基《異部宗輪論述記》：「依蘊處界假施設名者。謂我非即離蘊。處界亦爾。然世說言色是我。乃至法亦是我。但依蘊等假施設此我名。我實非蘊等。」

^ 智昇《開元釋教錄》：「長房內典等錄有十八部論一卷亦云諦譯。今尋文句非是諦翻。既與部執本同不合再出。今此刪之如別錄中述。」

^ 《三法度論》：「受名者取義也。因業及煩惱癡意計我是我所。是名受。」

^ 文字增補出自印順《說一切有部為主的論書與論師之研究》，第九章「上座別系分別論者」，第三節「被稱為分別論者的犢子部」，第二項「三法度論與僧伽斯那」。

^ 提婆設摩《識身論》：「謂契經中世尊善語善詞善說。如是五趣決定安立不相雜亂。謂捺落迦趣傍生趣鬼趣天趣人趣。」「……如是八種補特伽羅。決定安立不相雜亂。謂預流果能作證向。若預流果。乃至阿羅漢果。能作證向。」「……如是三聚決定安立不相雜亂。謂不定聚。邪性定聚。正性定聚。」「……如是三種補特伽羅。決定安立不相雜亂。謂學補特伽羅。無學補特伽羅。非學非無學補特伽羅。」

^ 世友菩薩《異部宗輪論》：「諸法若離補特伽羅。無從前世轉至後世。依補特伽羅可說有移轉。」
《大毘婆沙論》：「謂或有執補特伽羅。自體實有。如犢子部。彼作是說。我許有我。可能憶念本所作事。先自領納今自憶故。若無我者。何緣能憶本所作事。」迦多衍尼子《阿毘達磨發智論》：「補特伽羅。既不可得。又無前心往後心。理何緣能憶本所作事。答有情於法。由串習力。得如是同分智。隨所更事。能如是知。」

^ 龍樹《大智度論》：「般若波羅蜜中說諸法實相。諸法實相中無戲論垢濁故。名畢竟清淨。畢竟清淨故。能遍照一切五種法藏。所謂過去未來現在無為及不可說。」
龍樹《十住毘婆沙論》：「佛實是一切智人。何以故。凡一切法有五法藏。所謂過去法。未來法。現在法。出三世法。不可說法。唯佛如實遍知是法。」
訶梨跋摩《成實論》：「又汝法中說。可知法者。謂五法藏。過去未來現在無為。及不可說法。」

^ 龍樹《中論》：「若人說我相。如犢子部眾說。不得言色即是我。不得言離色是我。我在第五不可說藏中。如薩婆多部眾說。諸法各各相。是善是不善是無記。是有漏無漏有為無為等別。」

^ 《增一阿含經· 火滅品·第2經》：「有此二法涅槃界。云何為二。有餘涅槃界．無餘涅槃界。彼云何名為有餘涅槃界。於是。比丘滅五下分結。即彼般涅槃。不還來此世。是謂名為有餘涅槃界。彼云何名為無餘涅槃界。於是。比丘盡有漏成無漏。意解脫．智慧解脫。自身作證而自遊戲。生死已盡。梵行已立。更不受有。如實知之。是謂為無餘涅槃界。此二涅槃界。當求方便。至無餘涅槃界。」

^ ^15.0 ^15.1 《增支部·五集·149經、150經》：「「諸比丘！此等五法，能令時解脫之比丘退失。何等為五？即：樂於作業、樂於談話、樂於睡眠、樂於與眾雜處、不如實觀察解脫心是。諸比丘！此等五法，能令時解脫之比丘退失。」
《大毘婆沙論》：「如契經說。有五因緣令時解脫阿羅漢退。一營事業。二樂戲論。三和諍訟。四好遠行。五遇長病。」

^ 《中阿含經· 大品·福田經》：「世尊告曰。居士。世中凡有二種福田人。云何為二。一者學人。二者無學人。學人有十八。無學人有九。居士。云何十八學人。信行．法行．信解脫．見到．身證．家家．一種．向須陀洹．得須陀洹．向斯陀含．得斯陀含．向阿那含．得阿那含．中般涅槃．生般涅槃．行般涅槃．無行般涅槃．上流色究竟。是謂十八學人。居士。云何九無學人。思法．昇進法．不動法．退法．不退法。護法.護則不退.不護則退。實住法．慧解脫．俱解脫。是謂九無學人。」

^ 《雜阿含經·八二三經》：「如是知．如是見。斷三結。貪．恚．癡薄。得一種子道。若彼地未等覺者。得斯陀含。彼地未等覺者。名家家。彼地未等覺者。得須陀洹。彼地未等覺者。得隨法行。彼地未等覺者。得隨信行。」

^ 《三法度論》：「問云何第八若數者應第一不第八。初向後至阿羅漢云何此是阿羅漢耶。答不當觀。如人有八。兒彼非以長為第。八以幼為第。八如是世尊功德子有八。彼阿羅漢為長。諸漏已盡故。謂初向為幼。是以說第八。」

^ 《三法度論》：「中者。此二中。非一向從家至家般涅槃。亦不一向極七天人生般涅槃。而於中間般涅槃。」

^ 《三法度論》：「云何薄地。答薄地者。一來一種中。欲界結薄住。故曰薄地。」

^ 《三法度論》：「此三。一來一種中。一來者此終生天上。一來而般涅槃。一種者。受一有而般涅槃。增益功德故。中者此二俱。是三謂未離欲。」

^ 《雜阿含經·八二三經》：「如是知．如是見。斷五下分結。謂身見．戒取．疑．貪欲．瞋恚。斷此五下分結。得中般涅槃。於彼未等覺者。得生般涅槃。於彼未等覺者。得無行般涅槃。於彼未等覺者。得有行般涅槃。於彼未等覺者。得上流般涅槃。」

^ 《雜阿含經·九三六經》：「聖弟子一向於佛清淨信。乃至決定智慧。於正法．律如實知見。不得見到。是名聖弟子不墮惡趣。乃至信解脫。」

^ 《雜阿含經·九三六經》：「若聖弟子一向於佛清淨信。乃至決定智慧。不得八解脫身作證具足住。然於正法．律如實知見。是名聖弟子不墮惡趣。乃至見到。」

^ 《雜阿含經·九三六經》：「聖弟子一向於佛清淨信。乃至決定智慧。八解脫身作證具足住。而不見有漏斷。是名聖弟子不墮惡趣。乃至身證。」

^ 《中阿含經·大品·嗏帝經》：「復次三事合會入於母胎。父母聚集一處。母滿精堪耐。香陰已至。此三事合會入於母胎。」
《中阿含經· 七法品·善人往經》：「復次。比丘行當如是。我者無我。亦無我所。當來無我。亦無我所。已有便斷。已斷得捨。有樂不染。合會不著。行如是者。無上息跡慧之所見。然未得證。比丘行如是。往至何所。譬若如鐵洞燃俱熾。以椎打之。迸火飛空。從上來還。未至地滅。當知比丘亦復如是。少慢未盡。五下分結已斷。得中般涅槃。是謂第三善人所往至處。世間諦如有。」
《雜阿含經·九五七經》：「佛告婆蹉。眾生於此處命終。乘意生身生於餘處。當於爾時。因愛故取。因愛而住。故說有餘。」
《阿毘達磨發智論》：「如說四有。謂本有死有中有生有。云何本有。答除生分死分諸蘊中間諸有。云何死有。答死分諸蘊。云何中有。答除死分生分諸蘊中間諸有。云何生有。答生分諸蘊。」
《大毘婆沙論》：「問應理論者依何量故說有中有。答依至教量。如契經說。入母胎者要由三事俱現在前。一者母身是時調適。二者父母交愛和合。三健達縛正現在前。除中有身何健達縛。前蘊已壞何現在前。故健達縛即是中有。又經說有中般涅槃。中有若無。此依何立。餘經復說。此身已壞餘身未生意成有情依止於愛而施設取。世尊既說此身已壞餘身未生意成有情依愛立取。故知中有決定非無。若無中有意成有情名何所表。又說過難證有中有。謂從此洲歿生北俱盧等。若無中有此身既滅彼身未生中間應斷。是則彼身本無而有。此身亦則本有而無。法亦應爾。本無而有有已還無。勿有斯過故有中有。」
《三法度論》：「問非為重說耶。答不界異故。離欲界及離色界故。是二種盡除中陰。非有無色界中陰。」

^ 《雜阿含經·八二三經》：「如是知．如是見。欲有漏心解脫．有有漏心解脫．無明有漏心解脫。解脫知見。我生已盡。梵行已立。所作已作。自知不受後有。」

^ 《雜阿含經·九三六經》：「聖弟子一向於佛清淨信。乃至決定智慧。不得八解脫身作證具足住。然彼知見有漏斷。是名聖弟子不墮惡趣。乃至慧解脫。」

^ ^29.0 ^29.1 《雜阿含經·七一〇經》：「貪欲染心者。不得不樂。無明染心者。慧不清淨。是故。比丘。離貪欲者心解脫。離無明者慧解脫。若彼比丘離貪欲。心解脫。得身作證。離無明。慧解脫。是名比丘斷愛縛．結。慢無間等。究竟苦邊。

^ ^30.0 ^30.1 《中阿含經·因品·大因經》：「阿難。若有比丘彼七識住及二處知如真。心不染著。得解脫者。是謂比丘阿羅訶。名慧解脫。復次。阿難。有八解脫。云何為八。色觀色。是謂第一解脫。復次。內無色想外觀色。是謂第二解脫。復次。淨解脫身作證成就遊。是謂第三解脫。復次。度一切色想。滅有對想。不念若干想。無量空處。是無量空處成就遊。是謂第四解脫。復次。度一切無量空處。無量識處。是無量識處成就遊。是謂第五解脫。復次。度一切無量識處。無所有處。是無所有處成就遊。是謂第六解脫。復次。度一切無所有處。非有想非無想處。是非有想非無想處成就遊。是謂第七解脫。復次。度一切非有想非無想處想。知滅解脫。身作證成就遊。及慧觀諸漏盡知。是謂第八解脫。阿難。若有比丘彼七識住及二處知如真。心不染著。得解脫。及此八解脫。順逆身作證成就遊。亦慧觀諸漏盡者。是謂比丘阿羅訶。名俱解脫。」
《長阿含經·大緣方便經》：「阿難。復有八解脫。云何八。色觀色。初解脫。內無色想。觀外色。二解脫。淨解脫。三解脫。度色想。滅有對想。不念雜想。住空處。四解脫。度空處。住識處。五解脫。度識處。住不用處。六解脫。度不用處。住有想無想處。七解脫。滅盡定。八解脫。阿難。諸比丘於此八解脫。逆順遊行。入出自在。如是比丘得俱解脫。」

^ 《雜阿含經·九三六經》：「聖弟子於佛一向淨信。於法．僧一向淨信。於法利智．出智．決定智。八解脫具足身作證。以智慧見。有漏斷知。如是聖弟子不趣地獄．畜生．餓鬼。不墮惡趣。說阿羅漢俱解脫。」

^ 《雜阿含經·七一經》：「是名比丘阿羅漢。（1）盡諸有漏。（2）所作已作。（3）已捨重擔。（4）逮得己利。（5）盡諸有結。（6）正智心解脫。」

^ 《三法度論》：「阿羅漢者是說供養名。堪受供養故曰阿羅漢。問誰堪受。答為一切眾生。故說阿羅漢。」

^ 《雜阿含經·一〇九一經》(S.4.23. Godhika)：「時。有尊者瞿低迦。住王舍城仙人山側黑石室中。獨一思惟。不放逸行。修自饒益。時受意解脫身作證。數數退轉。一．二．三．四．五．六反退。還復得。時受意解脫身作證。尋復退轉。彼尊者瞿低迦作是念。我獨一靜處思惟。不放逸行。精勤修習。以自饒益。時受意解脫身作證。而復數數退轉。乃至六反。猶復退轉。我今當以刀自殺。莫令第七退轉。」

^ 《三法度論》：「俱解脫二。一得具解脫。二不具。俱解脫者。信及慧。已得此二故勝。」
《四阿鋡暮抄解》：「俱分解脫二。盡解脫報。不盡解脫報。俱分解脫名念解脫慧解脫。是二增去義彼義。」

[编辑] 參見

三彌底部論

[编辑] 外部連結

三法度論初探

显示▼ 查 · 論 · 編大正新修大藏經·釋經論部、毗曇部

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

2个分类:

釋經論部

犢子部

夜柔吠陀

维基百科，自由的百科全书

夜柔吠陀（Yajurveda；梵文：यजुर्वेदः 是由yajus「祭祀」和veda「知識」兩個詞根構成的復合詞）漢譯名稱為祭祀明論，是四大吠陀經之第三部。內容著重於禮拜及牲禮等的宗教儀式。

夜柔吠陀主要分為兩卷集著：白夜柔吠陀以及黑夜柔吠陀（「白」是指本文與釋文區分清楚，「黑」是指本文與釋文分辨不清）。兩者都包含宗教儀式的必要韻文，後者卻額外包含儀式的註解散文與施行細則，而這散文也開梵語散文體裁之先河。

夜柔吠陀（公元前1200－900）。書中說：「如果你從無限中移走或添加一部分，剩下的還是無限。」

分類:粒子物理學

粒子物理學是研究組成物質和射線的基本粒子以及它們之間的相互作用的物理學的一個分支。

此頁面分類的主條目是粒子物理學。

相關的維基共享資源：

粒子物理學

子分類

本分類包含下列19個子分類，共19個子分類。

F

[×] 反物質‎ (10個頁面)

L

[+] 量子力學‎ (14個分類， 148個頁面)

Z

[×] 自然單位‎ (12個頁面)

原

[+] 原子核物理學‎ (11個分類， 64個頁面)

同

[×] 同步輻射設施‎ (6個頁面)

味

[×] 味量子數‎ (3個頁面)

基

[×] 基本相互作用‎ (6個頁面)

散

[×] 散射‎ (13個頁面)

標

[×] 標準模型‎ (8個頁面)

粒

[+] 粒子‎ (1個分類)

[+] 粒子加速器‎ (1個分類， 29個頁面)

[×] 粒子探測器‎ (7個頁面)

[×] 粒子物理學家‎ (16個頁面)

[×] 粒子物理學小作品‎ (25個頁面)

粒續

[×] 粒子統計學‎ (5個頁面)

量

[+] 量子場論‎ (9個分類， 61個頁面)

[×] 量子數‎ (7個頁面)

[×] 量子電動力學‎ (9個頁面)

[+] 量子色動力學‎ (1個分類， 9個頁面)

"粒子物理學"分類中的頁面

本分類包含下列44個頁面，共有44個頁面。

對稱性 (物理學)

维基百科，自由的百科全书

（重定向自规范对称性）

對稱性（symmetry）是現代物理學中的一個核心概念，它泛指規範對稱性（gauge symmetry，或局域對稱性local symmetry）和整體對稱性（global symmetry）。它是指一個理論的拉格朗日量或運動方程在某些變數的變化下的不變性。如果這些變數隨時空變化，這個不變性被稱為規範對稱性，反之則被稱為整體對稱性。物理學中最簡單的對稱性例子是牛頓運動方程的伽利略變換不變性和麥克斯韋方程的洛倫茲變換不變性和相位不變性。

數學上，這些對稱性由群論來表述。上述例子中的群分別對應著伽利略群，洛倫茲群和 $U (1)$ 群。對稱群為連續群和分立群的情形分別被稱為連續對稱性（continuous symmetry)和分立對稱性(discrete symmetry)。德國數學家外爾(Hermann Weyl)是把這套數學方法運用於物理學中並意識到規範對稱重要性的第一人。1950年代楊振寧和米爾斯意識到規範對稱性可以完全決定一個理論的拉格朗日量的形式，並構造了核作用的 $S U (2)$ 規範理論。從此，規範對稱性被大量應用於量子場論和粒子物理模型中。在粒子物理的標準模型中，強相互作用，弱相互作用和電磁相互作用的規範群分別為 $S U (3)$ ， $S U (2)$ 和 $U (1)$ 。除此之外，其他群也被理論物理學家廣泛地應用，如大統一模型中的 $S U (5)$ ， $S O (10)$ 和 $E 6$ 群，超弦理論中的 $S O (32)$ 和 $E_8\times E_8$ 群。

整體對稱性在粒子物理和量子場論的發展中也起著非常重要的角色，如強相互作用的手征對稱性（chiral symmetry）。規範和整體對稱性的破缺是粒子物理和凝聚態理論的重要概念。

[编辑] 守恆定律與對稱性的關係

主條目：諾特定理

物理系統的每一個對稱性都有相對的守恆定律。諾特定理就是概括這關系的重要定理。它指出物理系統包含的每一個對稱性都代表此系統有某相對的物理量守恆。反過來說：物理系統有某守恆性質就代表它帶其相對的對稱性。例如，空間位移對稱造成動量守恆，而時間平移對稱造成能量守恆。

以下列表總結各對稱和相對的守恆量：

類型	不變性	守恆量
Proper orthochronous 勞侖茲對稱	時間平移 (時間同質性)	能量
	空間平移 (空間同質性)	直線動量
	空間旋轉 (各向同性)	角動量
分立對稱	P, 座標倒置	宇稱（鏡像對稱）
	C, 反粒子共軛	Charge Parity
	T, 時間反演	time parity
	CPT	product of parities
內部對稱 (不取決於時空座標)	U(1) 規范轉換	電荷數
	U(1) 規范轉換	輕子數
	U(1) 規范轉換	超電荷（hypercharge）
	U(1)_Y 規范轉換	weak hypercharge
	U(2) [U(1)xSU(2)]	電弱力
	SU(2) 規范轉換	同位旋
	SU(2)_L 規范轉換	弱原子力同位旋
	PxSU(2)	G-parity
	SU(3) "卷繞數"	重子數
	SU(3) 規范轉換	quark color
	SU(3) (approximate)	夸克味
	S((U2)xU(3)) U(1)xSU(2)xSU(3)	標準模型

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

3个分类:

量子場論

粒子物理學

對稱

對稱性破缺

维基百科，自由的百科全书

對稱性破缺是量子場論中的重要概念，指理論的對稱性為真空所破壞。它包含兩種情形—自發對稱性破缺（spontaneous symmetry breaking)(動力學對稱性破缺是自發對稱性破缺的一個特例。)以及顯性對稱破缺。它們在理論物理模型中都有重要應用。著名例子分別為標準模型中的希格斯機制和超導物理中的BCS理論。

被真空解破壞的對稱性可以是整體或局域對稱性，對稱群可以是分立或連續的。

[编辑] 參閱

南部-戈德斯通定理

希格斯機制

自發對稱性破缺

動力學對稱性破缺

顯性對稱破缺

玻色子

维基百科，自由的百科全书

玻色子（英語：boson）是依隨玻色-愛因斯坦統計，自旋為整數的粒子。玻色子不遵守泡利不相容原理，在低溫時可以發生玻色-愛因斯坦凝聚。

玻色子包括：

膠子 - 強相互作用的媒介粒子，自旋為1，有8種

光子 - 電磁相互作用的媒介粒子，自旋為1，只有1種

W 及 Z 玻色子 - 弱相互作用的媒介粒子，自旋為1，有3種

引力子 - 引力相互作用的媒介粒子，自旋為2，只有1種，尚未被發現

希格斯玻色子 - 尚未被發現

介子 - 由兩個費米子——夸克組成的強子。

由偶數個核子組成的原子核。因為質子和中子都是費米子，故含偶數個核子的原子核是自旋為整數的玻色子。

聲子 - 請參閱固體物理學

[编辑] 參閱

費米子

玻色-愛因斯坦統計

規範玻色子

隐藏▲

查 · 論 · 編

粒子

基本粒子

費米子	夸克：u · u · d · d · c · c · s · s · t · t · b · b 輕子：e^- · e⁺ · μ^- · μ⁺ · τ^- · τ⁺ · ν_e · v_e · ν_μ · v_μ · ν_τ · v_τ

玻色子	規範玻色子：γ · g · W^± · Z⁰

複合粒子

強子	重子/核子/超子：p · p · n · n · Δ · Λ · Σ · Ξ · Ω · 介子/夸克偶素：π · K · ρ · D · J/ψ · Υ

其它	原子核 · 原子 · 奇異原子：電子偶素 · 渺子偶素 · 介子原子 · 超子原子 · 反氫 · 介子核 · 超核 · 重味超核 · 分子

假想的基本粒子

超對稱粒子	軸微子 · 膠微子 · 光微子 · 引力微子 · W微子 · Z微子 · 希格斯微子 · 中性微子 · 超費米子：超輕子 · 超夸克

其它	大質量弱相互作用粒子(WIMP) · 惰性中微子 · 加速子 · 快子 · 軸子 · 引力子 · 希格斯玻色子 · X · Y · W' · Z'

假想的複合粒子

奇異強子	奇異重子：五夸克態 · 雙重子態 · 奇異介子：膠球 · 混雜態 · 四夸克態

其它	介子分子

準粒子

聲子 · 激子 · 電漿子 · 電磁極化子 · 極子 · 磁振子

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

玻色子

湮滅

無窮

目錄

[编辑] 歷史

[编辑] 早期無限的觀點

[编辑] 文藝復興時代至近代

[编辑] 神學中的無窮

[编辑] 數學中的無窮

[编辑] 實分析中的無窮

[编辑] 無窮大和無窮小

[编辑] 無窮遠點

[编辑] 集合論中的無窮

[编辑] 無窮的虛數形式標記

[编辑] 無窮影象

[编辑] 參考條目

[编辑] 參考文獻

虛數

[编辑] 視頻講解（英文）

[编辑] 參考

[编辑] 參看

閔考斯基時空

目錄

[编辑] 標準基底

[编辑] 因果結構

[编辑] 誤解

[编辑] 相關條目

封閉類時曲線

目錄

[编辑] 光錐

[编辑] 廣義相對論

[编辑] 相關條目

[编辑] 參考文獻

[编辑] 外部連結

中文數字

目錄

[编辑] 一般數字

[编辑] 對周邊國家的影響

[编辑] 大數系統

[编辑] 腳註

[编辑] 參見

三法度論

目錄

[编辑] 篇章結構

[编辑] 犢子部宗義

[编辑] 補特伽羅論

[编辑] 補特伽羅實有論

[编辑] 第五法藏攝我論

[编辑] 阿羅漢有退論

[编辑] 第一義諦

[编辑] 二十七賢聖

[编辑] 引用

[编辑] 參見

[编辑] 外部連結

夜柔吠陀

分類:粒子物理學

子分類

F

L

Z

原

同

味

基

散

標

粒

粒 續

量

"粒子物理學"分類中的頁面

*

B

C

D

E

F

G

I

I 續

L

N

粒續