BY THE WAY~-莫非│愛情公寓交友網站與聊天室

一隻黑猩猩隨機地打字，只要時間足夠，必然可以打出法國國家圖書館中的每本書。

無限猴子定理的表述如下：讓一隻猴子在打字機上隨機地按鍵，當按鍵時間達到無窮時，幾乎必然能夠打出任何給定的文字，比如莎士比亞的全套著作。

在這裡，幾乎必然是一個有特定含義的數學術語，「猴子」也不是一隻真正意義上的猴子，它被用來比喻成一個可以產生無限隨機字母序列的抽象設備。這個理論說明把一個很大但有限的數看成無限的推論是錯誤的。猴子精確地通過鍵盤敲打出一部完整的作品比如說莎士比亞的哈姆雷特，在宇宙的生命周期中發生的機率也是極其低的，但並不是零。

這個理論的變化形式包括多個甚至無限多個打字員，以及目標文本從一個完整的圖書館到一個簡單的句子。這些表述可以追述到亞里士多德的《論產生和毀滅》和西塞羅的的《論神之本性》，經過布萊茲·帕斯卡和喬納森·斯威夫特，最後到現在的形象的打字員的表述形式。在20世紀早期，埃米爾·博雷爾和亞瑟·愛丁頓運用這個理論在統計力學基礎中闡述隱式時間標尺。

[编辑] 起源

無限猴子定理是來自埃米爾·博雷爾一本1909年出版談機率的書籍，當中介紹了「打字的猴子」的概念。這個定理是機率論中的柯爾莫哥洛夫的零一律的其中一個命題的例子。不過，當波萊爾在書中提出零一律的這個特例時，柯爾莫哥洛夫的一般敘述並未給出（柯爾莫哥洛夫那本機率論的著作直到1933年才出版）。

[编辑] 定義

[编辑] 普遍認同的觀點

關於此定理的敘述為：有無限隻猴子用無限的時間會產生特定的文章。其實不必要出現了兩件無限的事物，一隻猴子打字無限次已經足夠打出任何文章，而無限隻猴子則能即時產生所有可能的文章。

[编辑] 其他定義

其他取代的敘述，可能是用大英博物館或美國國會圖書館取代法國國家圖書館；另一個常見的版本是英語使用者常用的，就是猴子會打出莎士比亞的著作。

[编辑] 出處

這一典故的出處，喬納森·斯威夫特 1782年出版的的《格列佛遊記》，第三部分第五章，教授要其學生透過經常轉動機械把手產生一些隨機的字句，以建立所有科學知識的列表。

[编辑] 證明

[编辑] 直接證明

兩個獨立事件同時發生的機率等於其中每個事件單獨發生的機率的乘積。比如，在某一天雪梨下雨的可能性為0.3，舊金山地震的可能性是0.008（這兩個事件可以視為相互獨立的），那麼它們同時發生的機率是 0.3 × 0.008 = 0.0024。

假設一個打字機有50個鍵，想要打出的字是「banana」。隨機的打字時，打出第一個字母「b」的機率是 1/50，打出第二個字母「a」的機率也是 1/50 ，因為事件是獨立的，所以一開始就打出單詞「banana」的機率是：

(1/50) × (1/50) × (1/50) × (1/50) × (1/50) × (1/50) = (1/50)⁶,

這個機率小於150億分之1。同理，接下來繼續打出「banana」的機率也是(1/50)⁶。

所以，在給定的六個字母沒有打出「banana」的機率是1 − (1/50)⁶。因為每一段（6個字母）文字都是獨立的，連續n段都沒有打出「banana」的機率X_n是：

$X_n=\left(1-\frac{1}{50^6}\right)^n\,$

隨著n變大，X_n在變小。當n等於100萬時，X_n大約是0.9999（沒有打出「banana」的機率是99.99%）；但是當n等於100億時X_n大約是0.53（沒有打出「banana」的機率是53%）；當n等於1000億時X_n大約是0.0017（沒有打出「banana」機率是0.17%）;當n趨於無窮時X_n趨於零。這就是說，只要使n足夠大，X_n可以變得足夠小。^[1]^[2]

同樣的論證也可以說明在無限多的猴子中有至少一個會打出一段特定的文章。這裡X_n = (1 − (1/50)⁶)ⁿ，其中X_n表示在前n個猴子中沒有一個一次打出banana的機率。當我們有1000億隻猴子時，這個機率降低到0.17%，並且隨著猴子數量n趨於無窮大，沒有打出「banana」的機率X_n趨於0。

但是，在只有有限的時間和有限只猴子時，結論就大不一樣了。如果我們的猴子數量和可觀測宇宙中的基本粒子數量一樣多，大約10⁸⁰隻，每秒鐘打1000個字，持續打100倍於宇宙的生命長度的時間（大約10²⁰秒）有猴子能夠打出一本很薄的書的機率也接近與0。見下文：機率。

[编辑] 無限長的字元串

以上兩種情況可以擴展到所有的字元串：

給定一個無限長的字元串，其中的每一個字元都是隨機產生的，那麼任意有限的字元串都會作為一個子字元串出現在其中（事實上要出現無限多次）。

給定一個序列，其中有無限多個無限長的字元串，其中每一個字元串中的每一個字元都是隨機產生的，那麼任意有限的字元串都會出現在其中某些字元串的開頭（事實上是無限多個字元串的開頭）.

對於第二個定理，設E_k某給定字元串出現在第k個字元串開頭的事件。有固定的且不為零的機率p是這個事件發生，而且E_k是獨立的，所以：

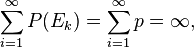
$\sum_{i=1}^\infty P(E_k) = \sum_{i=1}^\infty p = \infty,$

事件E_k發生無窮多次的機率是1。第一個定理可以類似地處理，先將無限長的字元串分割，使得每一段的長度和給定字元串相同，然後設E_k是第k段等於給定字元串的事件。^[3]

[编辑] 機率

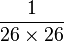不算標點符號、空格、大小寫，一個猴子隨機打字打出的第一個字母和哈姆雷特中相同的機率是 $\frac{1}{26}$ ，前兩個字母相同的機率是 $\frac{1}{676}$ （即 $\frac{1}{26\times26}$ ）。因為機率發生了指數爆炸，前20個字母相同的機率是 $26^{-20}=\frac{1}{19,928,148,895,209,409,152,340,197,376}\approx5.02\cdot10^{-29}$ 。而打出的字和哈姆雷特中的全部文本相同的機率降低到超出人們的想像。整部哈姆雷特大約有130,000個字母。^[4] 雖然有3.4×10^183,946分之一的機率一遍就正確地打出所有文本，在打出正確的文字之前平均需要輸入的字母數量也要3.4×10^183,946，^[5]或者包括標點符號，4.4×10^360,783。^[6]

即使可觀測宇宙中充滿了猴子一直不停地打字，能夠打出一部哈姆雷特的機率仍然少於10^183,800分之一。^[7]

[编辑] 現實

不過在現實中，猴子打出一篇像樣的文章的幾率是零，因為科學家經過反覆試驗後發現，猴子（或猩猩）在使用鍵盤時通常會連按某一個鍵或拍擊鍵盤，最終打出的文字不可能成為一個完整的句子。這是因為現實是非常大的有限，而不是嚴格意義上的無限。

[编辑] 注釋

^ This shows that the probability of typing "banana" in one of the predefined non-overlapping blocks of six letters tends to 1. In addition the word may appear across two blocks, so the estimate given is conservative.

^ Isaac, Richard E.. The Pleasures of Probability. Springer. 1995: 48–50. ISBN 038794415X. Isaac generalizes this argument immediately to variable text and alphabet size; the common main conclusion is on p.50.

^ The first theorem is proven by a similar if more indirect route in Gut, Allan. Probability: A Graduate Course. Springer. 2005: 97–100. ISBN 0387228330.

^ Using the Hamlet text from gutenberg, there are 132680 alphabetical letters and 199749 characters overall

^ For any required string of 130,000 letters from the set a-z, the average number of letters that needs to be typed until the string appears is (rounded) 3.4 × 10^183,946, except in the case that all letters of the required string are equal, in which case the value is about 4% more, 3.6 × 10^183,946. In that case failure to have the correct string starting from a particular position reduces with about 4% the probability of a correct string starting from the next position (i.e., for overlapping positions the events of having the correct string are not independent; in this case there is a positive correlation between the two successes, so the chance of success after a failure is smaller than the chance of success in general). The figure 3.4 × 10^183,946 is derived from n = 26¹³⁰⁰⁰⁰ by taking the logarithm of both sides: log₁₀(n) = 1300000×log₁₀(26) = 183946.5352, therefore n = 10^0.5352 × 10¹⁸³⁹⁴⁶ = 3.429 × 10¹⁸³⁹⁴⁶.

^ 26 letters ×2 for capitalisation, 12 for punctuation characters = 64, 199749×log₁₀(64) = 4.4 × 10^360,783.

^ Charles Kittel. Thermal Physics (2nd ed.). W. H. Freeman Company. 1980: 53. ISBN 0-7167-1088-9.

[编辑] 外部連結

The Million Monkey Room, October 2008, a satirical essay by D.R. Belz from The Baltimore Examiner^{[失效連結]}

Ask Dr. Math article, August 1998, Adam Bridge

The Parable of the Monkeys, a bibliography with quotations

Infinite Monkey / Dawkin's Weasel demo applet (in Monash University's Virtual Lab)

RFC 2795 - The Infinite Monkey Protocol Suite (IMPS)

無限猴子定理

目錄