维基百科，自由的百科全书

跳转到：导航, 搜索

「波」重定向至此。關於與其同名的其他主題，詳見「波 (消歧義)」。

水面波

波或波動是擾動或物理信息在空間上傳播的一種物理現象。擾動的形式是任意的。波的傳播速度總是有限的。除了電磁波和引力波能夠在真空中傳播外，大部分波如機械波只能在介質中傳播。

[编辑] 波的數學描述

在數學上，任何一個沿某一方向運動的函數形狀都可以認為是一個波。考慮一種最簡單的情況：二維平面波，波的形狀可以用 $xy$ 平面上的曲線 $y = f(x)$ 描述。

如果這個曲線沿著 $x$ 軸以 $\omega$ 的速度向右運動，不難看出，這樣的函數應該滿足如下方程： $y = f(x-\omega t)$

如果沿x軸以ω的速度向左運動，則為： $y = f(x+\omega t)$

以上兩個方程都滿足如下形式的微分方程：

$\frac{\partial ^2 f}{\partial t^2} = \omega ^2\frac{\partial ^2 f}{\partial x^2}$

這個方程稱為一維波動方程。

它的通解可以表示為：

$y(x,t)=f(x+\omega t) + g(x-\omega t)$

它表示一個向左傳播的波和一個向右傳播的波的疊加。

[编辑] 行進波

行進波，又稱為前進波，是一種在空間與時間裡的擾動，可以表達為

$y(z,t) = A(z,\ t)\sin (kz - \omega t + \phi)\,\!$ ；

其中， $A(z,\ t)\,\!$ 是波的振幅， $z\,\!$ 是位置， $t\,\!$ 是時間， $k\,\!$ 是波數， $\phi\,\!$ 是相數。

波的相速度 $v_p\,\!$ 可以表達為

$v_p = \frac{\omega}{k}= \lambda f\,\!$ ；

其中， $\lambda\,\!$ 是波長。

[编辑] 駐波

參見駐波

[编辑] 波的特徵參量

任何一種波都可以用如下的參量進行描述：

色散關係，即波的頻率ω與波矢量k之間的關係： $\omega=\omega(\boldsymbol{k})$ 。其中，波矢量的方向是垂直於波陣面的，其數值等於波數，即k=2π/λ。

波的相速度 $v_{p}=\omega/k$ 與群速度 $\boldsymbol{v}_g=\mathrm{d}\omega/\mathrm{d}\boldsymbol{k}$ 。相速度的方向與波矢量k的方向平行，而群速度表示波內能量轉移的大小和方向。

波的衰減率γ

波的偏振。可以是無偏振、線偏振、橢圓偏振或者是圓偏振。

[编辑] 能量

$E$ $=$ $0.5$ (mu△x) $(2pafR)$ $^2$

$E$ 是簡諧運動能量， $f$ 是頻率

$E = h\nu$

$E$ 是非力學波能量， $\nu$ 頻率

[编辑] 波的分類

波根據振動源的次數可以分為脈波和週期波，脈波的波源只對介質作一短暫的擾動。波通過介質時，介質中的質點在短暫振動後，隨即靜止於原位置。而週期波的波源對介質作連續有規律的振動。

波在均勻、無向性的介質中傳遞時，依介質的振動方向分可以分為縱波和橫波。縱波的特點是介質的振動方向與傳播方向相同，比如空氣中的聲波、地震波中的P波。橫波的特點是介質的振動方向與傳播方向垂直。如：電磁波、地震波中的S波。

如果在非均質介質中傳遞時，介質振動的行為就不是只有橫向與縱向兩種，亦存在像表面波、海浪這種類型的振動。譬如：雷利波其振動方式為橢圓形。

依波動傳遞需要介質來劃分，波可以分為機械波、電磁波。

物質波則是在近代物理中敘述物質具有粒子與波動的二元性，近一步的探討則認為物質波是物質在空間中分布的機率，如電子的軌域。

[编辑] 波的傳播

有些波的傳播需要介質，比如聲波等機械波。有些則不需要介質，在真空中也能傳播。如電磁波。

波在介質中傳播時，介質的質點並未隨波前進，而是在原處附近運動。

波的行進速度v為其頻率f和波長λ的乘積，即波長λ和週期T的比值： $v = f \lambda = \frac{\lambda}{T}$

波在繩子上傳播時，波的行進速度v（單位m/s）與繩子所受的張力F（單位N）及繩子的線密度μ（單位kg/m）有關： $v = \sqrt{F \over \mu}$

[编辑] 一維簡諧波

波可視為簡諧運動。

一種最基本、最常見的波是簡諧波。它可以表示為：

$f=Ae^{i(kx-\omega t)} \,$

其中 $k$ 是波數， $\omega$ 是角頻率， $A$ 是振幅。

波數倚賴於波長 $\lambda$ ， $k=\frac{2\pi}{\lambda}$ 。角頻率倚賴於周期 $T$ ， $\omega=\frac{2\pi}{T}$ 。

波速 $v=\frac{\omega}{k}$ 。

[编辑] 波的量子

每種波有相應的量子:

電磁波──光子

引力波──引力子

[编辑] 波的相關名詞

振幅(amplitude)

波形

波峰(crest)、波谷(trough)

波長(wavelength)：通常以λ表示。

週期(period)：通常以T表示。

頻率(frequency)：通常以f表示。

相速度

群速度

四維頻率

[编辑] 外部連結

橫行波Java模擬

縱行波Java模擬

弦線上駐波Java模擬

水波的干涉Java模擬

水波的繞射Java模擬

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

振動和波

波動方程式

维基百科，自由的百科全书

跳转到：导航, 搜索

汉漢▼

根據波動方程式的建模，一個脈衝在一根固定兩端的繩子上的運動

從一個點源發散出的球面波

波動方程式或稱波方程式（英語：wave equation）是一種重要的偏微分方程式，主要描述自然界中的各種的波動現象，包括橫波和縱波，例如聲波、光波和水波。波動方程式抽象自聲學，電磁學，和流體力學等領域。

歷史上許多科學家，如達朗伯特、歐拉、丹尼爾·白努利和拉格朗日等在研究樂器等物體中的弦振動問題時，都對波動方程式理論作出過重要貢獻。

波動方程式是雙曲形偏微分方程式的最典型代表，其最簡形式可表示為：關於位置x 和時間t 的純量函數u（代表各點偏離平衡位置的距離）滿足：

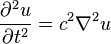
${ \partial^2 u \over \partial t^2 } = c^2 \nabla^2u$

這裡c通常是一個固定常數，代表波的傳播速率。在常壓、20°C的空氣中c為343米/秒（參見音速）。在弦振動問題中，c 依不同弦的密度大小和軸向張力不同可能相差非常大。而在半環螺旋彈簧（一種玩具，英文商標為 Slinky）上，波速可以慢到1米/秒。

在針對實際問題的波動方程式中，一般都將波速表示成可隨波的頻率變化的量，這種處理對應真實物理世界中的色散現象。此時，c 應該用波的相速度代替：

$v_\mathrm{p} = \frac{\omega}{k}.$

實際問題中對標準波動方程式的另一修正是考慮波速隨振幅的變化，修正後的方程式變成下面的非線性波動方程式：

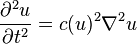
${ \partial^2 u \over \partial t^2 } = c(u)^2 \nabla^2u$

另需注意的是物體中的波可能是疊加在其他運動（譬如介質的平動，以氣流中傳播的聲波為例）上的。這種情況下，純量u 的表達式將包含一個馬赫因子（對沿流動方向傳播的波為正，對反射波為負）。

三維波動方程式描述了波在均勻各向同性彈性體中的傳播。絕大多數固體都是彈性體，所以波動方程式對地球內部的地震波和用於檢測固體材料中缺陷的超聲波的傳播能給出滿意的描述。在只考慮線性行為時，三維波動方程式的形式比前面更為複雜，它必須同時考慮固體中的縱波和橫波:

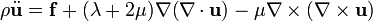
$\rho \ddot {\bold{u}} = \bold{f} + ( \lambda + 2\mu )\nabla(\nabla \cdot \bold{u}) - \mu\nabla \times (\nabla \times \bold{u})$

式中：

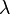$\lambda$ 和 $\mu$ 被稱為彈性體的拉梅常數（也叫「拉梅模量」，英文Lamé constants 或 Lamé moduli），是描述各向同性固體彈性性質的參數；

$\rho$ 表示密度；

$\bold{f}$ 是源函數（即外界施加的激振力）；

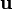$\bold{u}$ 表示位移；

注意在上述方程式中，激振力和位移都是向量，所以該方程式也被稱為向量形式的波動方程式。

其他形式的波動方程式還能在量子力學和廣義相對論理論中用到。

[编辑] 純量形式的一維波動方程式

[编辑] 波動方程式的推導

一維波動方程式可用如下的方式推導：一列質量為m的小質點，相鄰質點間用長度h的彈簧連接。彈簧的彈性係數（又稱「倔強係數」）為k：

其中u(x) 表示位於x的質點偏離平衡位置的距離。施加在位於x+h 處的質點m 上的力為：

$F_{Newton}=m \cdot a(t)=m \cdot {{\partial^2 \over \partial t^2}u(x+h,t)}$

$F_{Hooke} = F_{x+2h} + F_x = k \left [ {u(x+2h,t) - u(x+h,t)} \right ] + k[u(x,t) - u(x+h,t)]$

其中 $F_{Newton}$ 代表根據牛頓第二定律計算的質點慣性力， $F_{Hooke}$ 代表根據虎克定律計算的彈簧作用力。所以根據分析力學中的達朗伯特原理，位於x+h 處質點的運動方程式為：

$m{\partial^2u(x+h,t) \over \partial t^2}= k[u(x+2h,t)-u(x+h,t)-u(x+h,t)+u(x,t)]$

式中已註明u(x) 是時間t 的顯函數。

若N 個質點間隔均勻地固定在長度L = N h 的彈簧鏈上，總質量M = N m，鏈的總體勁度係數為K = k/N，我們可以將上面的方程式寫為：

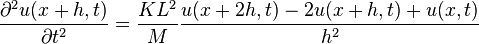
${\partial^2u(x+h,t) \over \partial t^2}={KL^2 \over M}{u(x+2h,t)-2u(x+h,t)+u(x,t) \over h^2}$

取極限 N 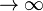$\rightarrow \infty$ , h $\rightarrow 0$ 就得到這個系統的波動方程式：

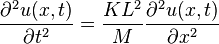
${\partial^2 u(x,t) \over \partial t^2}={KL^2 \over M}{ \partial^2 u(x,t) \over \partial x^2 }$

在這個例子中，波速 $c = \sqrt {\frac{{KL^2 }}{M}}$ 。

[编辑] 初值問題的解

一維純量形式波動方程式的一般解是由達朗伯特給出的。原方程式可以寫成如下的算子作用形式：

$\left[ \frac{\part}{\part t} - c\frac{\part}{\part x}\right] \left[ \frac{\part}{\part t} + c\frac{\part}{\part x}\right] u = 0.\,$

從上面的形式可以看出，若F 和G 為任意函數，那麼它們以下形式的組合

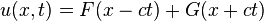
$u(x,t) = F(x-ct) + G(x+ct) \,$

必然滿足原方程式。上面兩項分別對應兩列行波（"行"與在"行動"中同音）——F 表示經過該點（x 點）的右行波，G 表示經過該點的左行波。為完全確定F 和G 的最終形式還需考慮如下初始條件：

$u(x,0)=f(x) \,$

$u_t(x,0)=g(x) \,$

經帶入運算，就得到了波動方程式著名的達朗伯特行波解，又稱達朗伯特公式：

$u(x,t) = \frac{f(x-ct) + f(x+ct)}{2} + \frac{1}{2c} \int_{x-ct}^{x+ct} g(s) ds$

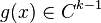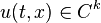在古典的意義下，如果 $f(x) \in C^k$ 並且 $g(x) \in C^{k-1}$ 則 $u(t,x) \in C^k$ 。但是，行波函數F和G 也可以是廣義函數，比如狄拉克δ函數。在這種情況下，行波解應被視作左行或右行的一個脈衝。

基本波動方程式是一個線性微分方程式，也就是說同時受到兩列波作用的點的振幅就是兩列波振幅的相加。這意味著可以通過把一列波分解成它的許多分量來分析其行為。傅立葉變換就是將一個波分解成正弦/餘弦分量的方法，因此在波動方程式的求解中很有效。

[编辑] 純量形式的三維波動方程式

三維波動方程式初值問題的解可以通過求解球面波波動方程式得到。求解結果可用於推導二維情況的解。

[编辑] 球面波

球面波方程式的形式不隨空間坐標系統的轉動而變化，所以可以將它寫成僅與距源點距離r 相關的函數。方程式的三維形式為：

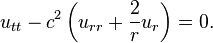
$u_{tt} - c^2 \left( u_{rr} + \frac{2}{r} u_r \right) =0. \,$

將方程式變形為：

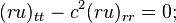
$(ru)_{tt} -c^2 (ru)_{rr}=0; \,$

此時，因變數ru 滿足一維波動方程式，於是可以利用達朗伯特行波法將解寫成：

$u(t,r) = \frac{1}{r} F(r-ct) + \frac{1}{r} G(r+ct), \,$

其中F 和G 為任意函數，可以理解為以速度c 從中心向外傳播的波和從外面向中心傳播的波。這類從點源傳出的波強度隨距點源距離r 衰減，並且屬於無後效波，可以清晰地搭載信號。這種波僅在奇數維空間中存在（原因將在下一小節中詳細解釋）。幸運的是，我們生活的空間是三維的，所以我們可以清晰地通過聲波和電磁波（都屬於球面波）來互相交流。

[编辑] 時間箭頭的討論

上面方程式的解裡面，分成了兩部分，一部分表示向外傳播的波，一部分則是向內。很明顯，只要將t換成-t，就可以在這兩部分之間轉換。這體現了原始方程式對於時間是對稱的，任意的一個解在時間軸上倒過來看仍然是一個解。

然而，我們所觀察到的實際的波，都是屬於向外傳播的。除非精心地加以調整，我們無法在自然界觀察到向內的波，儘管它們也是波動方程式的合法的解。

關於這個現象，引起了不少討論。有人認爲，實際上它們即使存在，也無法加以觀察。想想如果四周的光向一個物體集中，則因爲沒有光到達我們的眼睛，我們不可能看見這個物體或者發現這個現象（見參考文獻[2] ）。

[编辑] 廣義初值問題的解

波動方程式中u 是線性函數，並且不隨時間和空間坐標的平移而改變。所以我們可以通過平移與疊加球面波獲得方程式各種類型的解。令 φ(ξ,η,ζ) 為任意具有三個自變數的函數，球面波形F 為狄拉克δ函數（數學語言是：F 是一個在全空間積分等於1且非零區間收縮至原點的連續函數的弱極限）。設(ξ,η,ζ)位一族球面波的源點，r 為距源點的徑向距離，即：

$r^2 = (x-\xi)^2 + (y-\eta)^2 + (z-\zeta)^2. \,$

可定義

$U(t,x,y,z;\xi ,\eta ,\zeta ) = \frac{{\delta (r - ct)}}{{4\pi cr}}$

稱為三維波動方程式的影響函數，其意義為(ξ,η,ζ)點在t=0 時刻受到短促脈衝δ函數作用後向空間中傳出的波的影響，係數分母 4πc 是為方便後續處理而加上的。

若u 是這一族波函數的加權疊加，且權函數為 φ，則

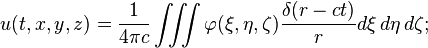
$u(t,x,y,z) = \frac{1}{4\pi c} \iiint \varphi(\xi,\eta,\zeta) \frac{\delta(r-ct)}{r} d\xi\,d\eta\,d\zeta; \,$

從δ函數的定義可知，u 還能寫成

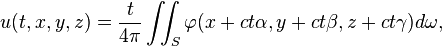
$u(t,x,y,z) = \frac{t}{4\pi} \iint_S \varphi(x +ct\alpha, y +ct\beta, z+ct\gamma) d\omega, \,$

式中α、β 和 γ 是單位球面S 上點的坐標，dω 為S 上的面積微元。該結果的意義為：u(t,x,y,z) 是以(x,y,z) 為圓心，ct 為半徑的球面上φ 的平均值的t 倍：

$u(t,x,y,z) = t M_{ct}[\phi]. \,$

從上式易得

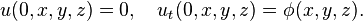
$u(0,x,y,z) = 0, \quad u_t(0,x,y,z) = \phi(x,y,z). \,$

平均值是關於t 的偶函數，所以若

$v(t,x,y,z) = \frac{\part}{\part t} \left( t M_{ct}[\psi] \right), \,$

那麼

$v(0,x,y,z) = \psi(x,y,z), \quad v_t(0,x,y,z) = 0. \,$

以上得出的便是波動方程式初值問題的解。從中可以看出，任意點P 在t 時刻受到的波擾動只來自以P 為圓心，ct 為半徑的球面上，而這個球的內部點在這一時刻對P 點的狀態完全沒有影響（因為它們的影響之前就已經傳過P 點了）。換一個角度分析，假設三維空間中任意點P' 在t=0 時刻受到一個脈衝擾動δ，那麼由此發出的球面波在傳過空間中的任意其它點Q 後，便再也不會對Q 的運動狀態產生影響，這就是在物理學中也非常著名的惠更斯原理（Huygens' principle），也稱為無後效現象，表示傳過的球面波不會留下任何後續效應。

下面我們便可以解釋上一小節中留下的問題了。事實上，前面所得到的球面波解僅在奇數維空間中存在。偶數維空間中波動方程式的解是彌散的，也就是說波陣面掠過區域仍然會受其影響。以下面的二維波動方程式（極坐標形式，注意和上一小節三維形式的差別）為例：

$u_{tt} - c^2 (u_{rr} + \frac{1}{r}u_r ) = 0$

可以從三維形式的解通過降維法得到二維波動方程式的影響函數：

$U(t,x - \xi ,y - \eta )=\begin{cases} \frac{1}{{2\pi c}}\frac{1}{{\sqrt {c^2 t^2 - r^2 } }}, & r \le ct \\ 0, & r > ct \end{cases}$

其中

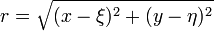
$r = \sqrt {(x - \xi )^2 + (y - \eta )^2 }$

設點M(x,y) 到點(ξ,η) 距離為d，那麼從影響函數中可以看出，當t >d /c 即初始擾動已傳過M 點後，M 仍在受到它的影響。二維球面波（柱面波）的這一性質決定了它不能作為傳遞信號的工具，因為這種波（事實上包括所有偶數維空間中的球面波）經過的點受到的是交織在一起的各個不同時刻的擾動。

[编辑] 純量形式的二維波動方程式

二維波動方程式的直角坐標形式為：

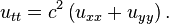
$u_{tt} = c^2 \left( u_{xx} + u_{yy} \right). \,$

如前所述，我們可以從三維波動方程式的解中將u 視為與其中一個自變數無關（降維法）來得到二維形式的解。將初始條件改寫為

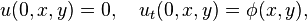
$u(0,x,y)=0, \quad u_t(0,x,y) = \phi(x,y), \,$

則三維形式的解就變成

$u(t,x,y) = tM_{ct}[\phi] = \frac{t}{4\pi} \iint_S \phi(x + ct\alpha,\, y + ct\beta) d\omega,\,$

其中 α 和 β 是單位球面上點的頭兩個坐標分量，dω 是球面上的面積微元。此積分可變換為在(x,y) 為中心， ct 為半徑的圓域D 上的積分：

$u(t,x,y) = \frac{1}{2\pi c} \iint_D \frac{\phi(x+\xi, y +\eta)}{\sqrt{(ct)^2 - \xi^2 - \eta^2}} d\xi\,d\eta. \,$

從這個結果也能得到上一小節最後的結論。

二維波動方程式解的一個例子是緊繃的鼓面的運動。

[编辑] 邊值問題

[编辑] 一維情形

一根自身繃緊，兩端分別固定於x=0 和x=L 的彈性弦在t>0 時刻，0 < x < L 上運動滿足波動方程式。在邊界點處，可以要求u 滿足各種邊界條件。通常遇到的邊界條件都可歸納成下列形式：

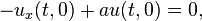
$-u_x(t,0) + a u(t,0) = 0, \,$

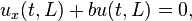
$u_x(t,L) + b u(t,L) = 0,\,$

其中a、b 非負。若要弦的兩端固定不動，對應上面式子中a、b 趨於無窮大。求解偏微分方程式的分離變數法要求尋找以下形式的解：

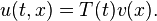
$u(t,x) = T(t) v(x).\,$

將上述假設形式代入原方程式中可以得到：

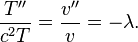
$\frac{T''}{c^2T} = \frac{v''}{v} = -\lambda. \,$

為使邊值問題有非平凡解，本徵值 λ 須滿足

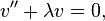
$v'' + \lambda v=0, \,$

$-v'(0) + a v(0) = 0, \quad v'(L) + b v(L)=0.\,$

這是固有值問題的斯圖姆-劉維爾理論的一個特例。若a、b 為正數，則對應的所有本徵值均為正數，方程式的解為三角函數。使u 和u_t 滿足平方可積條件的解可以通過適當選取u 和u_t 三角級數展開來求得。

[编辑] 多維情形

一維初始值-邊值理論可以拓展至任意維空間中。考慮m 維空間（坐標簡寫為x）中的域D ，B為D的邊界。當0<t 時，位於D 內的點x 滿足波動方程式。在D 的邊界上，解u 須滿足

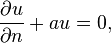
$\frac{\part u}{\part n} + a u =0, \,$

其中n 是B 上指向域外的法向向量，a 是定義在B 上的非負函數。要求u 在B 上始終為0的邊界條件相當於令a 趨於無窮。初始條件為

$u(0,x) = f(x), \quad u_t=g(x), \,$

其中f 和g 是定義在D 內的函數。這個問題可以通過將f 和g 展開成域D 內拉普拉斯算子滿足邊界條件的本徵函數系的疊加來求解（這是分離變數法的一般步驟）。也就是求解在域D 內滿足

$\nabla \cdot \nabla v + \lambda v = 0, \,$

在邊界B 上滿足

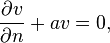
$\frac{\part v}{\part n} + a v =0, \,$

的本徵函數系v 。

在二維情形下，上述本徵函數系可以理解成繃緊地張在邊界B 上的鼓面的自由振動模態。若B 是一個圓，則這些本徵函數是關於極角自變數θ 的三角函數與關於極軸自變數r 的整階貝索函數的乘積。更詳細的說明參見英文版條目亥姆霍茲方程式。

在三維形式下，若邊界是空間中的球面，那麼本徵函數是關於球坐標下兩個極角自變數的球面調和函數，乘以關於徑向自變數ρ 的半奇數階貝索函數。

[编辑] 註釋

[编辑] 參考文獻

[1] 嚴鎮軍編，《數學物理方程式》，第二版，中國科學技術大學出版社，合肥，2002，第210頁~第224頁，ISBN 7-312-00799-6/O·177

[2] [英]胡·普賴斯著，肖巍譯，《時間之矢與阿基米德之點—物理學時間的新方向》，上海科學技術出版社，上海，2001， ISBN 7-5323-5737-6

[3] M. F. Atiyah, R. Bott, L. Garding, Lacunas for hyperbolic differential operators with constant coefficients I, Acta Math., 124 (1970), 109–189.

[4] M.F. Atiyah, R. Bott, and L. Garding, Lacunas for hyperbolic differential operators with constant coefficients II, Acta Math., 131 (1973), 145–206.

[5] R. Courant, D. Hilbert, Methods of Mathematical Physics, vol II. Interscience (Wiley) New York, 1962.

[编辑] 參看

聲波方程式

電磁波方程式

馬達變數

都卜勒效應

電磁學

光學

位相

薛丁格方程式

[编辑] 外部連結

線性波動方程式在EqWorld上：數學方程式的世界。

非線性波動方程式在EqWorld上：數學方程式的世界。

MISN-0-201 波動方程式及其解 (PDF) William C. Lane 為Project PHYSNET所著

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

5个分类:

數學物理

方程

偏微分方程

雙曲型偏微分方程

振動和波

辛幾何

维基百科，自由的百科全书

跳转到：导航, 搜索

辛幾何（Symplectic geometry），也叫辛拓撲（Symplectic topology），是微分幾何的一個分支。其研究對象為辛流形，亦即帶有閉非退化 2-形式的微分流形。辛拓撲源於經典力學的哈密頓表述，其中特定經典系統的相空間有辛流形的結構。

辛拓撲和研究有非退化對稱2階張量(稱為度量張量)的流形的黎曼幾何有一些相似和不同之處。不像黎曼的情況，辛流形沒有像曲率那樣的局部不變數。這是達布定理的一個結果，表明每一對辛流形是局部同構的。另一個和黎曼幾何的區別是不是所有的微分流形可以接受一個辛形式；有一些特定的拓撲限制。首先，流形必須是偶數維的。辛拓撲的很多工作就是以研究哪些流形可以有辛結構為中心的。

每個凱勒流形也是一個辛流形。直到1970年代，辛專家們還不確信是否有任何緊非Kähler辛流形存在，但從那以後又很多例子被構造出來(第一個由William Thurston給出)；特別的，Robert Gompf證明每個有限表示群都可以作為辛4維流形的基本群出現，這和凱勒的情形完全不同。

可以說大部分辛流形都是非凱勒的;所以沒有和辛形式相容的可積復結構。但是 Mikhail Gromov給出了一個重要的發現，就是辛流形可以接受很多相容的殆復結構，所以它們滿足複流形的所有假設，"除了"坐標變換函數必須是全純的這一條。

以幾乎復結構相容的映射到辛流形的黎曼曲面稱為偽全純曲線，格羅莫夫證明了該類曲線的緊緻性定理；這個結構導致了辛拓撲一個很大的子學科的發展。從格羅莫夫的理論產生的結果包括關於球到柱的辛嵌入的格羅莫夫非壓縮定理，和關於哈密頓流的不動點的個數的阿爾諾德的一個猜想的證明。這是由從Andreas Floer開始的幾個研究者(逐步推廣到更一般的情形)所證明的，Floer用格羅莫夫的方法引入了現在稱為Floer同調的概念。

偽全純曲線也是辛不變數的一個來源，這種不變數稱為Gromov-Witten不變數，原則上可以用來區分兩個不同的辛流形。

[编辑] 參看

辛流形

哈密頓力學

黎曼幾何

切觸幾何

[编辑] 參考

Dusa McDuff and D. Salamon, Introduction to Symplectic Topology, Oxford University Press, 1998. ISBN 0-19-850451-9.

A. T. Fomenko, Symplectic Geometry (2nd edition) (1995) Gordon and Breach Publishers, ISBN 2-88124-901-9. (Provides an undergrad level introduction.)

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

辛拓撲

相空間

维基百科，自由的百科全书

跳转到：导航, 搜索

汉漢▼

一具有收斂穩定性的動態系統之相空間

在數學與物理學中，相空間是一個用以表示出一系統所有可能狀態的空間；系統每個可能的狀態都有一相對應的相空間的點。這個方法在1901年由約西亞·威拉德·吉布斯提出。

以力學系統來說，相空間通常是由位置變數以及動量變數所有可能值所組成。將位置變數與動量變數畫成時間的函數有時稱為相空間圖，簡稱「相圖」（phase diagram)）。然而在物質科學（physical sciences）中，「相圖」這詞更常是留給一化學系統用以表示其熱力學相態多種穩定性區域的圖表，為壓力、溫度及化學組成等等之函數。

在一相空間中，系統的每個自由度或參數可以用多維空間中的一軸來代表。對於系統每個可能的狀態，或系統參數值允許的組合，可以在多維空間描繪成一個點。通常這樣的描繪點連接而成的線可以類比於系統狀態隨著時間的演化。最後相圖可以代表系統可以存在的狀態，而它的外型可以輕易地闡述系統的性質，這在其他的表示方法則不那麼顯明。一相空間可有非常多的維度。舉例來說，一氣體包含許多分子，每個分子在x、y、z方向上就要有3個維度給位置與3個維度給速度，可能還需要額外的維度給其他的性質。

在古典力學中，相空間坐標由廣義坐標q_i以及其共軛的廣義動量p_i所組成。研究由許多系統所構成的系綜在此空間中的運動是屬於古典統計力學的範疇。

這是與數學相關的小作品。你可以透過編輯或修訂擴充其內容。

相空間是一個與物理學相關的小作品。你可以通過編輯或修訂擴充其內容。

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

2个分类:

動態系統

哈密頓力學

分類:動態系統

跳转到：导航, 搜索

動態系統（或稱動力系統）研究運動方程的解，主要對象是力學領域的方程，此外也包括行星軌道、電路問題與生物學中出現的偏微分方程。混沌系統是當前研究熱點之一。

詳見主條目 動態系統。

相關的維基共享資源：

動態系統

子分类

本分類包含下列14個子分類，共14個子分類。

不

[×] 不动点‎ (12个页面)

哈

[×] 哈密顿力学‎ (33个页面)

振

[+] 振动和波‎ (3个分类， 48个页面)

[+] 振荡‎ (1个分类， 2个页面)

控

[+] 控制工程‎ (1个分类， 2个页面)

旋

[+] 旋涡‎ (3个分类， 1个页面)

混

[×] 混沌映射‎ (2个页面)

[+] 混沌理论‎ (3个分类， 9个页面)

熱

[+] 热力学‎ (21个分类， 125个页面)

熵

[+] 熵‎ (2个分类)

自

[×] 自组织‎ (3个页面)

遍

[×] 遍歷理論‎ (4个页面)

非

[+] 非平衡態熱力學‎ (1个分类， 12个页面)

[+] 非线性物理学‎ (3个分类， 6个页面)

"動態系統"分类中的页面

本分類包含下列27個頁面，共有27個頁面。

度量張量

维基百科，自由的百科全书

跳转到：导航, 搜索

在黎曼幾何裡面，度量張量，物理學譯為度規張量，是指一用來衡量度量空間中距離及角度的二階張量。

當選定一個局域坐標系統 $x^i$ ，度量張量可以矩陣表示，記作為G或g。而 $g_{ij}$ 記號傳統地表示度量張量的協變分量(亦為「矩陣元素」)。以下我們用愛因斯坦求和約定來代表隱含的求和。

一小段弧線長度定義如下，其中參數定為t，t由a到b:

$L = \int_a^b \sqrt{ g_{ij}{dx^i\over dt}{dx^j\over dt}}dt$

兩個切向量的夾角 $\theta$ , $U=u^i{\partial\over \partial x_i}$ 和 $V=v^i{\partial\over \partial x_i}$ ，定義為:

$<br /> \cos \theta = \frac{g_{ij}u^iv^j}<br /> {\sqrt{ \left| g_{ij}u^iu^j \right| \left| g_{ij}v^iv^j \right|}}<br />$

在歐幾里得幾何中，為流形光滑嵌入導入度量張量，由以下方程式計算得出:

$G = J^T J$

$J$ 表示崁入的雅可比矩陣，它的轉置為 $J^T$

[编辑] 例子

[编辑] 歐幾里德幾何度量

二維歐幾里德度量張量:

$g_{ij} = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}$

弧線長度轉為熟悉微積分方程式:

$L = \int_a^b \sqrt{ (dx^1)^2 + (dx^2)^2}$

在其他坐標系統的歐氏度量:

極坐標系: $(x^1, x^2)=(r, \theta)$

$g_{ij} = \begin{bmatrix} 1 & 0 \\ 0 & (x^1)^2\end{bmatrix}$

圓柱坐標系: $(x^1, x^2, x^3)=(r, \theta, z)$

$g_{ij} = \begin{bmatrix} 1 & 0 & 0\\ 0 & (x^1)^2 & 0 \\ 0 & 0 & 1\end{bmatrix}$

球坐標系: $(x^1, x^2, x^3)=(r, \phi, \theta)$

$g_{ij} = \begin{bmatrix} 1 & 0 & 0\\ 0 & (x^1)^2 & 0 \\ 0 & 0 & (x^1\sin x^2)^2\end{bmatrix}$

平面閔可夫斯基空間: $(x^0, x^1, x^2, x^3)=(t, x, y, z)\,$

$g_{\mu\nu} = \eta_{\mu\nu} \equiv \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}$

在一些習慣中，與上面相反地，時間t 的度規分量取正號而空間 (x,y,z) 的度規分量取負號，故矩陣表示為：

$g_{\mu\nu} = \eta_{\mu\nu} \equiv \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{bmatrix}$

[编辑] 參看

偽黎曼度量

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

2个分类:

度量幾何

張量

史瓦西度規

维基百科，自由的百科全书

跳转到：导航, 搜索

汉漢▼

廣義相對論

$G_{\mu \nu} + \Lambda g_{\mu \nu}= {8\pi G\over c^4} T_{\mu \nu}\,$

入門、數學形式

显示▼基礎概念

显示▼現象

显示▼方程式

显示▼進階理論

显示▼愛因斯坦場方程式的解

显示▼科學家

查 • 論 • 編 • 歷

史瓦西度規（Schwarzschild metric），又稱史瓦西幾何、史瓦西解，是卡爾·史瓦西^註於1915年針對廣義相對論的核心方程式——愛因斯坦場方程式——關於球狀物質分布的解。此解所對應的幾何，可以是球狀星球以外的時空，也可以是靜止不旋轉、不帶電荷之黑洞（稱「史瓦西黑洞」）的時空幾何。

[编辑] 史瓦西度規

利用史瓦西座標，史瓦西度規可以表示成如下形式：

$\mathrm{d}s^{2} = c^2 \left(1-\frac{2GM}{c^2 r} \right) \mathrm{d}t^2 - \left(1-\frac{2GM}{c^2 r}\right)^{-1}\mathrm{d}r^2 - r^2 \mathrm{d}\Omega^2,$

其中 $G$ 是重力常數， $M$ 解釋為產生重力的物體之質量，而

$\mathrm{d}\Omega^2 = \mathrm{d}\theta^2+\sin^2\theta \mathrm{d}\phi^2\,$

是二維球面(2-sphere)上的標準度規（即：立體角的標準單元）。

常數

$r_s = \frac{2GM}{c^2}$

稱作史瓦西半徑，在史瓦西解中扮演關鍵角色。

史瓦西度規實際上是真空場方程式的解析解，意思上表示其僅在重力來源物體以外的地方能夠成立。也就是說，對一半徑 $R$ 之球狀體，此解僅在 $r > R$ 時成立。然而，若 $R$ 少於史瓦西半徑 $r_s$ ，此時解描述的是一個黑洞（見下文）。為了要描述重力來源物體內部與外部兩者的重力場，史瓦西解必須跟一個適當的內部解在 $r = R$ 處相洽。

注意到當 $M\to 0$ 或 $r \rightarrow\infty$ ，史瓦西度規近似為閔可夫斯基時空

$\mathrm{d}s^{2} = c^2 \mathrm{d}t^2 - \mathrm{d}r^2 - r^2 \mathrm{d}\Omega^2.\,$

直觀上說，這樣的結果是合理的：既然遠離了重力來源物體，時空理應變得近乎平直。具有這樣性質的度規稱作是「漸進平直 (asymptotically flat)」。

[编辑] 相關條目

愛因斯坦場方程式

黑洞

史瓦西度規是一個與物理學相關的小作品。你可以通過編輯或修訂擴充其內容。

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

廣義相對論的精確解

基本粒子

维基百科，自由的百科全书

跳转到：导航, 搜索

基本粒子指人們認知的構成物質的最小最基本的單位。但是因為物理學的不斷發展，人類對物質構成的認知逐漸深入，因此基本粒子的定義隨時間也是有所變化的。目前在粒子物理學中，標準模型理論認為的基本粒子可以分為夸克、輕子、規範玻色子和希格斯粒子四大類。標準模型理論之外也有理論認為可能存在質量非常大的超粒子。

基本粒子列表

[编辑] 基本粒子定義的變化

傳統上（20世紀前、中期）的基本粒子指質子、中子、電子、光子和各種介子，這是當時人類所能探測的最小粒子。而現代物理學發現質子、中子、介子都是由更加基本的夸克和膠子構成。同時人類也發現了性質和電子類似的一系列輕子，還有性質和光子、膠子類似的一系列規範玻色子。這些是現代的物理學所理解的基本粒子。

[编辑] 基本粒子的分類

[编辑] 費米子

主條目：費米子

[编辑] 夸克

目前的實驗顯示共存在6種夸克（quark），和他們各自的反粒子。這6種夸克又可分為3「代」。他們是

第一代：u（上夸克） d（下夸克）

第二代：s（奇異夸克） c（魅夸克）

第三代：b（底夸克） t（頂夸克）

它們的質量關係是 $m_u \simeq m_d < m_s < m_c < m_b < m_t$ 。另外值得指出的是，他們之所以未能被早期的科學家發現，原因是夸克決不會單獨存在（頂夸克例外，但是頂夸克太重了而衰變又太快，早期的實驗無法製造）。他們總是成對的構成介子，或者3個一起構成質子和中子這一類的重子。這種現象稱為夸克禁閉理論。這就是為什麼早期科學家誤以為介子和重子是基本粒子。

[编辑] 輕子

共存在6種輕子（lepton)和他們各自的反粒子。其中3種是電子和與它性質相似的 $μ$ 子和 $τ$ 子。而這三種各有一個相伴的中微子。他們也可以分為三代：

第一代：e（電子） $ν e$ （電子中微子）

第二代： $μ$ （ $μ$ 子） $ν μ$ （ $μ$ 子中微子）

第三代： $τ$ （ $τ$ 子） $ν τ$ （ $τ$ 子中微子）

[编辑] 玻色子

主條目：玻色子

[编辑] 規範玻色子

這是一類在粒子之間起媒介作用、傳遞相互作用的粒子。之所以它們稱為「規範玻色子」，是因為它們與基本粒子的理論楊-米爾斯規範場理論有很密切的關係。

自然界一共存在四種相互作用，因此也可以把規範玻色子分成四類。

引力相互作用：引力子（graviton）

電磁相互作用：光子（photon）

弱相互作用（使原子衰變的相互作用）：W 及 Z 玻色子，共有3種： $W +, W -, Z 0$

強相互作用（夸克之間的相互作用）：膠子（gluon）

粒子物理學已經證明電磁相互作用和弱相互作用來源於宇宙早期能量極高時的同一種相互作用，稱為「弱電相互作用」。有很多粒子物理學家猜想在更早期宇宙更高能量（普朗克尺度）時很可能這四種相互作用全都是統一的，這種理論稱為「大統一理論」。但是目前因為加速器能夠達到的能量相對普朗克尺度仍然非常的低，所以很難驗證。而大統一理論目前主要的發展方向是超弦理論。

[编辑] 膠子

膠子是強相互作用的媒介子，帶有色與反色並由於色緊閉而從未被探測器觀察到過。不過，像單個的夸克一樣，它們產生強子噴注。在高能態環境下電子與正電子的湮沒有時產生三個噴註：一個夸克，一個反夸克和一個膠子是最先證明膠子存在的證據

[编辑] 希格斯粒子

希格斯粒子（Higgs）是粒子物理標準模型中唯一還沒有在加速器上產生出來的粒子。粒子物理學家們認為希格斯粒子與其他粒子的相互作用使其他粒子具有質量。相互作用越強質量就越大。希格斯粒子本身質量極大，目前的加速器能量還無法達到，而理論的計算也比較困難。物理學家們普遍希望能夠在2008年將要開始運行的大型強子對撞機上產生出希格斯粒子。

標準模型預言存在2種希格斯粒子： $H +$ 和 $H 0$ ，但是也有很多科學家提出其他的可能性。

[编辑] 標準模型理論以外的理論性粒子

[编辑] 超對稱粒子

除了以上這些實驗已經證明的基本粒子之外，理論粒子物理學家為了解釋某些現有理論無法解釋的實驗現象，而猜想我們的宇宙中可能存在超對稱粒子。它們質量非常地大（相對一般粒子如質子而言），因此現有的加速器還無法製造他們。但是因為量子漲落的存在，因此它們可能在非常短的時間間隔內和非常小的機率下與我們可見的粒子發生相互作用，因此它們可以間接地探測到。目前每種粒子都被認為存在對應的超對稱粒子。並且被用來解釋某些物理現象。例如夸克的超對稱粒子用來解釋正反粒子數目的不對稱，以及中微子的超對稱粒子用來解釋為什麼中微子的質量如此之小（但不是等於0）。

[编辑] 假想的粒子

有一些粒子，僅僅是理論學家的假想，而基本沒有確切的實驗根據，因此可能宇宙中根本不存在。這些粒子的提出或者只是為了給某些現有的現象作一種可能的解釋，或者僅僅是這種粒子如果存在也不會破壞現有的物理定律，因此我們沒有理由相信他們一定不存在而已。例如某些科學家認為占宇宙總能量約25%的「暗物質」，就是一種與其他物質作用極其微弱的但是有質量的粒子(WIMP)。此外也有一些理論研究某些速度永遠大於光速的速子，以及磁單極子或加速子等等。

显示▼ 查 · 論 · 編粒子

显示▼ 查 · 論 · 編基本粒子 - 輕子

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

1个分类:

基本粒子

基本交互作用

维基百科，自由的百科全书

（重定向自基本交互作用）

跳转到：导航, 搜索

汉漢▼

基本交互作用為物質間最基本的交互作用，常稱為自然界四力或宇宙基本力。迄今為止觀察到的所有關於物質的物理現象，在物理學中都可藉助這四種基本交互作用的機製得到描述和解釋。

名稱	相對強度 (以強交互作用為準)	性質 (對距離的作用大小)	作用的範圍(米)	傳遞交互作用的中間玻色子
強交互作用	1	1/r⁷	10^-15	膠子
電磁交互作用	1/137	1/r²	無限大	光子
弱交互作用	10^-13	1/r^{5 - 7}	10^-18	W 及 Z 玻色子(W^±,Z⁰)
引力交互作用	10^-39	1/r²	無限大	重力子

大統一理論認為：強交互作用、弱交互作用和電磁交互作用可以統一成一種交互作用，目前統一弱交互作用和電磁交互作用的電弱統一理論已經獲得實驗證實。

[编辑] 重力交互作用

主條目：萬有引力

重力交互作用，簡稱重力或引力，是四個基本交互作用中最弱的，但是同時又是作用範圍最大的（不會如電磁力一般相互抵銷）。但當距離增大，重力交互作用的影響力就會遞減，假設兩物件的相互距離為r，其作用力則可以1/r²的計算式推論出來。不像其他的交互作用，重力可以廣泛地作用於所有的物質。由於其廣泛的作用範圍，當物質質量為極大，物質有關的屬性以及與物質的帶電量有時可以相對地忽略。

而由於其廣泛的作用範圍，引力可以解釋一些大範圍的天文現象，比如：銀河系、黑洞和宇宙膨脹；以及基本天文現象例如：行星的公轉；還有一些生活常識例如物體下落、很重的物體好像被固定在地上、人不能跳得太高等。

萬有引力是第一種被數學理論描述的交互作用。在古代，亞里士多德建立了具有不同質量的物體是以不同的速度下落的理論。到了科學革命時期，伽利略·伽利萊用試驗推翻了這個理論－如果忽略空氣阻力，那麼所有的物體都會以相同的速度落向地面。艾薩克·牛頓看到蘋果掉落時發現地心引力，進而引伸出萬有引力定律 (1687年) ，是一個用來描述通常重力行為非常好的近例。在1915年, 阿爾伯特·愛因斯坦完成了廣義相對論，將重力用另一種方式描述－時空幾何，並指出引力是空間與時間彎曲的一種影響。

如今，一個活躍的領域正致力於用一個使用範圍更廣的理論來統一廣義相對論和量子力學－大統一理論。在量子力學中，一個在量子引力理論中設想的粒子－引力子被廣泛地認為是一個傳遞引力的粒子。引力子仍是假想粒子，目前還沒有被觀測到。

儘管廣義相對論在非量子力學限制的情況下較精確地描述了引力，但是仍有不少描述萬有引力的替代理論。這些在物理學界嚴格審視下的理論都是為了減少一些廣義相對論的局限性，而目前觀測工作的焦點就是確定什麼理論修正廣義相對論的局限性是可能的。

但是，最近的研究似乎顯示，萬有引力並不是基本力，而是熵力。^[1]

[编辑] 電磁交互作用

主條目：電磁交互作用

世上大部分物質都具有電磁力，而磁與電是電磁力的其中一種表現模式。例如電荷異性相吸、同性相斥的特性是其中之一。電磁力和重力一樣，其作用影響範圍是無限大的。

[编辑] 強交互作用

主條目：強交互作用

強交互作用又稱為強核力，所有存在宇宙中的物體都是由原子構成，而原子核是由中子和質子組成。中子沒有電荷，而質子則帶正電；但需要牽引力把它們結合在一起，而強交互作用就是這種「牽引力」

[编辑] 弱交互作用

主條目：弱交互作用

弱交互作用，或弱核力，可以說是核能另一種來源，主要是核子產生之天然輻射，四種交互作用中，弱交互作用只比引力強一點。

[编辑] 參見

^ On the Origin of Gravity and the Laws of Newton（英文）

強交互作用

弱交互作用

電磁交互作用

重力交互作用

交互作用

標準模型理論

電弱統一理論

大統一理論

萬有理論

宇宙速度

显示▼ 查 · 論 · 編物理學的基本交互作用

查看条目评分

给本文评分

这是什么？

可信度

客观性

完整性

可读性

我非常了解与本主题相关的知识（可选）

3个分类:

基本相互作用

力學

核能

波

目錄

[编辑] 波的數學描述

[编辑] 行進波

[编辑] 駐波

[编辑] 波的特徵參量

[编辑] 能量

[编辑] 波的分類

[编辑] 波的傳播

[编辑] 一維簡諧波

[编辑] 波的量子

[编辑] 波的相關名詞

[编辑] 外部連結

波動方程式

目錄

[编辑] 純量形式的一維波動方程式

[编辑] 波動方程式的推導

[编辑] 初值問題的解

[编辑] 純量形式的三維波動方程式

[编辑] 球面波

[编辑] 時間箭頭的討論

[编辑] 廣義初值問題的解

[编辑] 純量形式的二維波動方程式

[编辑] 邊值問題

[编辑] 一維情形

[编辑] 多維情形

[编辑] 註釋

[编辑] 參考文獻

[编辑] 參看

[编辑] 外部連結

辛幾何

[编辑] 參看

[编辑] 參考

相空間

分類:動態系統

子分类

不

哈

振

控

旋

混

熱

熵

自

遍

非

"動態系統"分类中的页面

D

H

X

Z

岡

分

分 续

多

希

龐

弗

敏

時

李

極

歐

流

混

穩

自

過

鍵

階

度量張量

[编辑] 例子

[编辑] 歐幾里德幾何度量

[编辑] 參看

史瓦西度規

[编辑] 史瓦西度規

[编辑] 相關條目

基本粒子

目錄

分续